| 比赛场次 | 511 |
|---|---|
| 比赛名称 | 近5年noip/csp题目回顾 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-06-25 08:30:00 |
| 结束时间 | 2022-06-26 17:30:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 只有历年比赛题才最接近比赛题。 |
| 题目名称 | 最小环(民间数据) |
|---|---|
| 输入输出 | ring.in/out |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 256 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
WWWWWWAWAWWWWWWWWWWW |
1.295 s | 0.00 MiB | 10 |
【题目描述】
给定一个长度为 $n$ 的正整数序列 $a_i$,下标从 $1$ 开始编号。我们将该序列视为一个首尾相邻的环,更具体地,对于下标为 $i$,$j$ $(i \le j)$ 的两个数 $a_i , a_j$,它们的距离为 $min ( j - i , i + n - j )$。
现在再给定 $m$ 个整数 $k_1 , k_2 , \ldots , k_m$,对每个 $k_i$ $( i = 1 , 2 , \ldots , m)$,你需要将上面的序列 $a_i$ 重新排列,使得环上任意两个距离为 $k_i$ 的数字的乘积之和最大。
【输入格式】
第一行两个正整数 $ n , m$,表示序列长度与询问数。
接下来一行 $n$ 个正整数表示 $a_i$。
接下来 $m$ 行每行一个非负整数表示 $k_i$。
【输出格式】
共 $m$ 行,每行一个整数表示答案。
【样例输入】
6 3 1 2 3 4 5 6 0 1 2
【样例输出】
91 82 85
【样例解释】
$k_i = 0$ 时:答案为每个数平方的和。
$k_i = 1$ 时:一种最优方案:$\{3,1,2,4,6,5\}$,答案为:
$$3 × 1 + 1 × 2 + 2 × 4 + 4 × 6 + 6 × 5 + 5 × 3 = 82$$
$k_i = 2$ 时:一种最优方案:$\{3,6,1,4,2,5\}$,答案为:
$$3 × 1 + 1 × 2 + 2 × 3 + 6 × 4 + 4 × 5 + 5 × 6 = 85$$
【数据范围与提示】
对于所有测试数据:$1 \le m \le n \le 2 \times 10^5,0 \le k \le \lfloor \frac{n}{2}\rfloor ,1 \le a_i \le 10^5$。
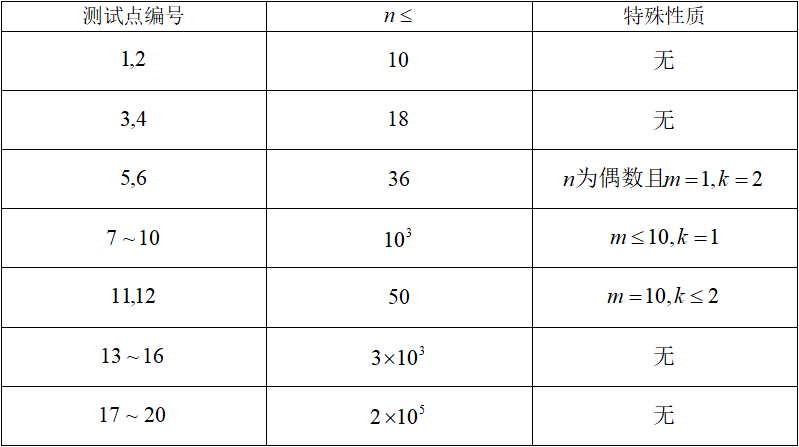
每个测试点的具体限制见下表:
【来源】
NOI Online2020 提高组 第一轮 Task 3
数据来源 @Knight @Mr.Chang