| 比赛场次 | 511 |
|---|---|
| 比赛名称 | 近5年noip/csp题目回顾 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-06-25 08:30:00 |
| 结束时间 | 2022-06-26 17:30:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 只有历年比赛题才最接近比赛题。 |
| 题目名称 | 交通规划 |
|---|---|
| 输入输出 | traffic.in/out |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|
【题目描述】
给定一个平面上$n$条水平直线和$m$条垂直直线,它们相交形成$n$行$m$列的网格,从上到下第$r$条水平直线和从左到右第$c$条垂直直线之间的交点称为格点$(r,c)$。网格中任意两个水平或垂直相邻的格点之间的线段称为一条边,每条边有一个非负整数边权。
进行$T$次询问,每次询问形式如下:
给出$k$($T$次询问的$k$可能不同)个附加点,每个附加点位于一条从网格边缘向外出发的射线上。所有从网格边缘向外出发的射线按左上-右上-右下-左下-左上的顺序依次编号为$1$到$2n+2m$,如下图:
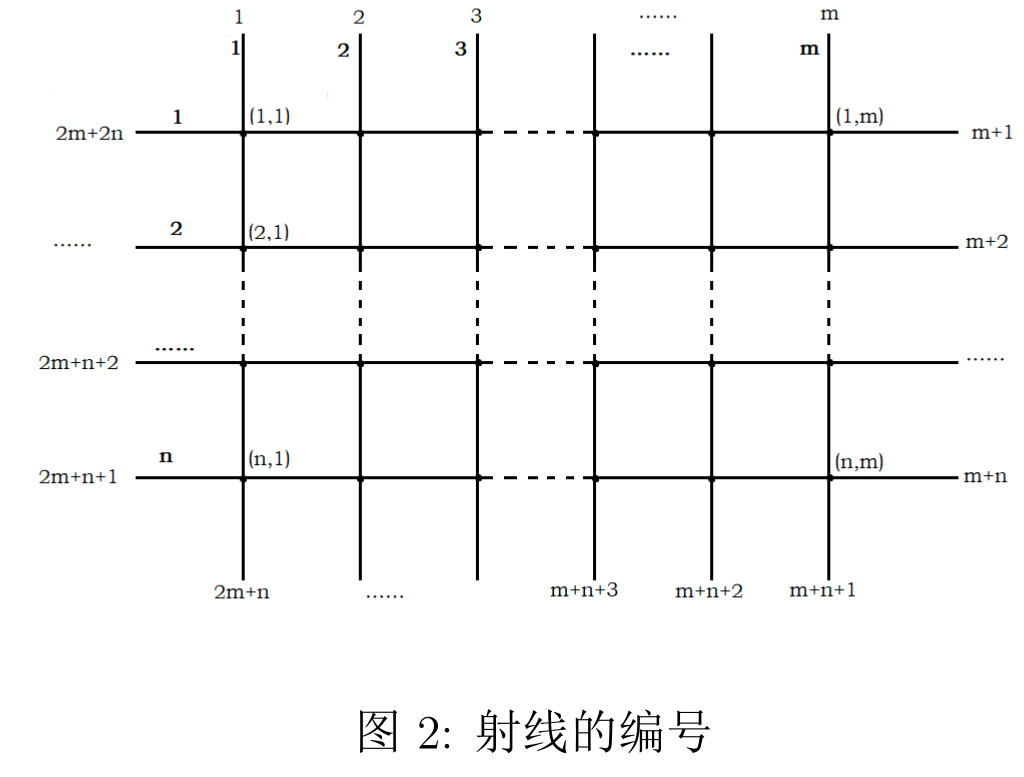
对于每次询问,不同附加点所在的射线互不相同。每个附加点和最近的格点之间的线段也称为一条边,也有非负整数边权(注意,在角上的格点有可能和两个附加点同时相连)。
给定每个附加点的颜色(黑色或者白色),请你将网格内每个格点的颜色染成黑白二者之一,并使得所有两端颜色不同的边的边权和最小。请输出这个最小的边权和。
【输入格式】
第一行 3 个正整数$n,m,T$分别表示水平、垂直直线的数量,以及询问次数。
接下来$n-1$行,每行$m$个非负整数。其中第$i$行的第$j$个非负整数$x1_{i,j}$表示$(i,j)$和$(i + 1,j)$间的边权。
接下来$n$行,每行$m-1$个非负整数。其中第$i$行的第$j$个非负整数$x2_{1,j}$表示$(i,j)$和$(i,j + 1)$间的边权。
接下来依次输入$T$组询问。第$i$组询问开头为一行一个正整数$k_i$表示这次询问附加点的总数。接下来$k_i$行每行三个非负整数。其中第$j$行依次为$x3_{i,j},p_{i,j},t_{i,j}$表示第$i$个附加点和相邻格点之间的边权、所在的射线编号以及附加点颜色(0为白色,1为黑色)。保证同一组询问内$p_{i,j}$互不相同。
每行的多个整数由空格分隔。
【输出格式】
输出$T$行,第$i$行输出一个非负整数,表示第$i$次询问染色之后两端颜色不同的边权和的最小值。
【样例1输入】
2 3 1 9 4 7 3 8 10 5 2 19 3 1 17 9 0
【样例1输出】
12
【样例1解释】
最优方案:$(1,3),(1,2),(2,3)$为黑色;$(1,1),(2,1),(2,2)$为白色。
【样例2/3/4/5】
【数据规模与约定】

对于所有数据,$2\leq n,m\leq 500,1\leq T\leq 50,1\leq k\leq \min\{2(n+m),50\},1\leq \sum_{i=1}^Tk_i\leq 50,$ $0\leq x\leq 10^6,1\leq p\leq 2(n+m),t\in\{0,1\}$。
保证对于每个$i\in\{1,T\},p_{i,j}$互不相同。
【来源】
CSP2021 提高组 Task4