| 比赛场次 | 511 |
|---|---|
| 比赛名称 | 近5年noip/csp题目回顾 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-06-25 08:30:00 |
| 结束时间 | 2022-06-26 17:30:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 只有历年比赛题才最接近比赛题。 |
| 题目名称 | 廊桥分配 |
|---|---|
| 输入输出 | airport.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|
【题目描述】
当一架飞机抵达机场时,可以停靠在航站楼旁的廊桥,也可以停靠在位于机场边缘的远机位。乘客一般更期待停靠在廊桥,因为这样省去了坐摆渡车前往航站楼的周折。然而,因为廊桥的数量有限,所以这样的愿望不总是能实现。
机场分为国内区和国际区,国内航班飞机只能停靠在国内区,国际航班飞机只能停靠在国际区。一部分廊桥属于国内区,其余的廊桥属于国际区。
L 市新建了一座机场,一共有$n$个廊桥。该机场决定,廊桥的使用遵循“先到先得” 的原则,即每架飞机抵达后,如果相应的区(国内/国际)还有空闲的廊桥,就停靠在廊桥,否则停靠在远机位(假设远机位的数量充足)。该机场只有一条跑道,因此不存在两架飞机同时抵达的情况。
现给定未来一段时间飞机的抵达、离开时刻,请你负责将$n$个廊桥分配给国内区和国际区,使停靠廊桥的飞机数量最多。
【输入格式】
输入的第一行包含 3 个正整数$n,m_1,m_2$分别表示廊桥的个数、国内航班飞机的数量、国际航班飞机的数量。
接下来$m_1$行是国内航班的信息,第$i$行包含 2 个正整数$a_{1,i}, b_{1,i}$,分别表示一架国内航班飞机的抵达、离开时刻。
接下来$m_2$行是国际航班的信息,第$i$行包含 2 个正整数$a_{2,i}, b_{2,i}$,分别表示一架国际航班飞机的抵达、离开时刻。
每行的多个整数由空格分隔。
【输出格式】
输出一个正整数,表示能够停靠廊桥的飞机数量的最大值。
【样例1输入】
3 5 4 1 5 3 8 6 10 9 14 13 18 2 11 4 15 7 17 12 16
【样例1输出】
7
【样例1解释】
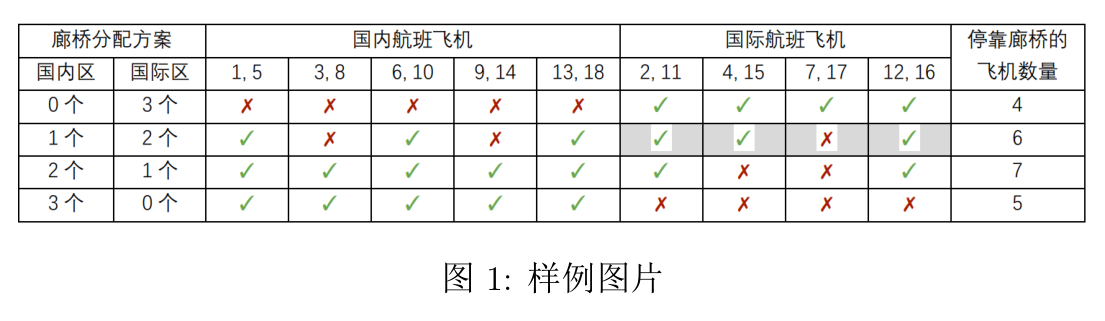 在图中,我们用抵达、离开时刻的数对来代表一架飞机,如(1, 5)表示时刻 1 抵达、时刻 5 离开的飞机;用√表示该飞机停靠在廊桥,用×表示该飞机停靠在远机位。
在图中,我们用抵达、离开时刻的数对来代表一架飞机,如(1, 5)表示时刻 1 抵达、时刻 5 离开的飞机;用√表示该飞机停靠在廊桥,用×表示该飞机停靠在远机位。
我们以表格中阴影部分的计算方式为例,说明该表的含义。在这一部分中,国际区有2 个廊桥,4 架国际航班飞机依如下次序抵达:
1.首先(2, 11)在时刻2抵达,停靠在廊桥
2.然后(4, 15)在时刻4抵达,停靠在另一个廊桥
3.接着(7, 17)在时刻7抵达,这时前 2 架飞机都还没离开、都还占用着廊桥,而国际区只有2 个廊桥,所以只能停靠远机位
4.最后(12, 16)在时刻 12 抵达,这时(2,11)这架飞机已经离开,所以有 1 个空闲的廊桥,该飞机可以停廊桥
根据表格中的计算结果,当国内区分配 2 个廊桥、国际区分配 1 个廊桥时,停靠廊桥的飞机数量最多,一共7架。
【样例2输入】
2 4 6 20 30 40 50 21 22 41 42 1 19 2 18 3 4 5 6 7 8 9 10
【样例2输出】
4
【样例2解释】
当国内区分配 2 个廊桥、国际区分配 0 个廊桥时,停靠廊桥的飞机数量最多,一共 4 架,即所有的国内航班飞机都能停靠在廊桥。
需要注意的是,本题中廊桥的使用遵循“先到先得”的原则,如果国际区只有 1 个廊桥,那么将被飞机(1, 19)占用,而不会被(3, 4)、(5, 6)、(7, 8)、(9,10)这 4 架飞机先后使用。
【样例3】
【数据规模与约定】
对于 20% 的数据,$1\leq n\leq 100,1\leq m_1+m_2\leq 100$。
对于 40% 的数据,$1\leq n\leq 5000,1\leq m_1+m_2\leq 5000$。
对于100% 的数据,$1\leq n\leq 100000,1\leq m_1+m_2\leq 100000$。
所有$a_{1,i}, b_{1,i}, a_{2,i}, b_{2,i}$为数值不超过$10^8$的互不相同的正整数。
保证$\forall i\in[1,n],a_{1,i}<b_{1,i},a_{2,i}<b_{2,i}$。
【来源】
CSP2021 提高组 Task1