| 比赛场次 | 511 |
|---|---|
| 比赛名称 | 近5年noip/csp题目回顾 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-06-25 08:30:00 |
| 结束时间 | 2022-06-26 17:30:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 只有历年比赛题才最接近比赛题。 |
| 题目名称 | 如何正确地排序 |
|---|---|
| 输入输出 | sort.in/out |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|
【题目描述】
有一个 $m\times n$ 的数据 $a_{i,j}$。
定义:$$f(i,j)=\min_{k=1}^{m}(a_{k,i}+a_{k,j})+\max_{k=1}^{m}(a_{k,i}+a_{k,j})$$
你需要求出 $\sum_{i=1}^{n}\sum_{j=1}^{n}f(i,j)$。
【输入格式】
第一行两个正整数 $m,n$。
接下来 $m$ 行,每行 $n$ 个正整数表示 $a_{i,j}$。
【输出格式】
一行一个正整数,表示答案。
【样例输入】
3 5 1 7 2 2 7 9 10 4 10 3 7 7 8 10 2
【样例输出】
564
【样例说明】
以 $f(3,5)$ 为例:
$f(3,5)=\max(a_{1,3}+a_{1,5},a_{2,3}+a_{2,5},a_{3,3}+a_{3,5})+\min(a_{1,3}+a_{1,5},a_{2,3}+a_{2,5},a_{3,3}+a_{3,5})$
$=\max(9,7,10)+\min(9,7,10)=10+7=17$
下面给出 $f(i,j)$ 的数表,第 $i$ 行第 $j$ 列表示 $f(i,j)$:
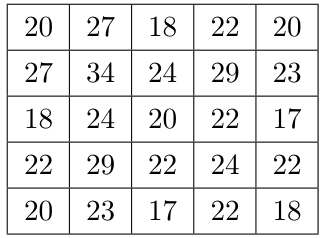
它们的和是答案 $564$。
【数据规模与约定】
对于所有测试点:$2\leq m\leq 4,1\leq n\leq 2\times 10^5,1\leq a_{i,j}\leq 2\times 10^5$。
每个测试点的具体限制见下表:
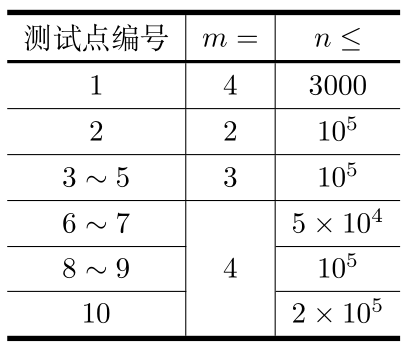
【来源】
NOI Online2022 1st 提高组 T3