| 比赛场次 | 511 |
|---|---|
| 比赛名称 | 近5年noip/csp题目回顾 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-06-25 08:30:00 |
| 结束时间 | 2022-06-26 17:30:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 只有历年比赛题才最接近比赛题。 |
| 题目名称 | 括号序列 |
|---|---|
| 输入输出 | bracket.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
WWWTTWTTWTTTTTTTTTTT |
15.016 s | 4.59 MiB | 0 |
【题目描述】
小 w 在赛场上遇到了这样一个题:一个长度为$n$且符合规范的括号序列,其有些位置已经确定了,有些位置尚未确定,求这样的括号序列一共有多少个。
身经百战的小 w 当然一眼就秒了这题,不仅如此,他还觉得一场正式比赛出这么简单的模板题也太小儿科了,于是他把这题进行了加强之后顺手扔给了小c。
具体而言,小 w 定义“超级括号序列”是由字符(、)、*组成的字符串,并且对于某个给定的常数$k$,给出了“符合规范的超级括号序列”的定义如下:
1、()、(S)均是符合规范的超级括号序列,其中S表示任意一个仅由不超过$k$个字符*组成的非空字符串(以下两条规则中的S均为此含义);
2、如果字符串A和B均为符合规范的超级括号序列,那么字符串AB、ASB均为符合规范的超级括号序列,其中AB表示把字符串A和字符串B拼接在一起形成的字符串;
3、如果字符串A为符合规范的超级括号序列,那么字符串(A)、(SA)、(AS)均为符合规范的超级括号序列。
4、所有符合规范的超级括号序列均可通过上述3条规则得到。
例如,若$k = 3$ ,则字符串((**()*(*))*)(***)是符合规范的超级括号序列,但字符串*()、(*()*)、((**))*)、(****(*))均不是。特别地,空字符串也不被视为符合规范的超级括号序列。
现在给出一个长度为 $n$ 的超级括号序列,其中有一些位置的字符已经确定,另外一些位置的字符尚未确定(用?表示)。小 w 希望能计算出:有多少种将所有尚未确定的字符一一确定的方法,使得得到的字符串是一个符合规范的超级括号序列?
可怜的小c并不会做这道题,于是只好请求你来帮忙。
【输入格式】
第 1 行,2 个正整数 $n,k$ 。
第 2 行,一个长度为$n$且仅由(、)、*、?构成的字符串S。
【输出格式】
输出一个非负整数表示答案对$10^9+7$取模的结果。
【样例1输入】
7 3 (*??*??
【样例1输出】
5
【样例1解释】
如下几种方案是符合规范的:
(**)*() (**(*)) (*(**)) (*)**() (*)(**)
【样例2输入】
10 2 ???(*??(?)
【样例2输出】
19
【样例3/4】
【数据规模与约定】
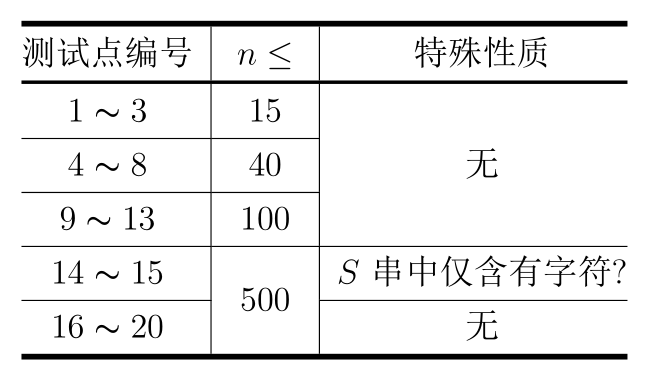
对于 100% 的数据,$1\leq k\leq n\leq 500$。
【来源】
CSP2021 提高组 Task2