| 比赛场次 | 511 |
|---|---|
| 比赛名称 | 近5年noip/csp题目回顾 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-06-25 08:30:00 |
| 结束时间 | 2022-06-26 17:30:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 只有历年比赛题才最接近比赛题。 |
| 题目名称 | 微信步数 |
|---|---|
| 输入输出 | walk.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|
【题目描述】
小 C 喜欢跑步,并且非常喜欢在微信步数排行榜上刷榜,为此他制定了一个刷微信步数的计划。
他来到了一处空旷的场地,处于该场地中的人可以用 $k$维整数坐标 ($a_1 ,a_2 ,\cdots,a_k$)来表示其位置。场地有大小限制,第 $i$ 维的大小为 $w_i$ ,因此处于场地中的人其坐标应满足 $1 \leq a_i \leq w_i$($1 \leq i \leq k$)。
小 C 打算在接下来的 $P=w_1\times w_2\times \cdots \times w_k$天中,每天从场地中一个新的位置出发,开始他的刷步数计划(话句话说,他将会从场地中每个位置都出发一次进行计划)。
他的计划非常简单,每天按照事先规定好的路线行进,每天的路线由 $n$ 步移动构成,每一步可以用 $c_i$ 与 $d_i$ 表示:若他当前位于 ($a_1 ,a_2 ,\cdots, a_{c_i},\cdots,a_k$),则这一步他将会走到 ($a_1 ,a_2 ,\cdots, a_{c_i}+d_i,\cdots,a_k$),其中 $1\leq c_i\leq k,d_i\in \{-1,1\}$。小 C 将会不断重复这个路线,直到他走出了场地的范围才结束一天的计划。(即走完第 n 步后,若小 C 还在场内,他将回到第 1 步从头再走一遍)。
小 C 对自己的速度非常有自信,所以他并不在意具体耗费的时间,他只想知道 P天之后,他一共刷出了多少步微信步数。请你帮他算一算。
【输入格式】
第一行两个用单个空格分隔的整数 $n,k$。分别表示路线步数与场地维数。
接下来一行 $k$ 个用单个空格分隔的整数 $w_i$,表示场地大小。
接下来 $n$ 行每行两个用单个空格分隔的整数 $c_i,d_i$ ,依次表示每一步的方向,具体意义见题目描述。
【输出格式】
仅一行一个整数表示答案。答案可能很大,你只需要输出其对 $10^9+7$ 取模后的值。
若小 C 的计划会使得他在某一天在场地中永远走不出来,则输出一行一个整数 $-1$。
【样例1输入】
3 2 3 3 1 1 2 -1 1 1
【样例1输出】
21
【样例1解释】
从 (1,1) 出发将走 2 步,从 (1,2) 出发将走 4 步,从 (1,3) 出发将走 4 步。
从 (2,1) 出发将走 2 步,从 (2,2) 出发将走 3 步,从 (2,3) 出发将走 3 步。
从 (3,1) 出发将走 1 步,从 (3,2) 出发将走 1 步,从 (3,3) 出发将走 1 步。
共计 21 步。
【样例2输入】
5 4 6 8 6 5 3 1 2 1 1 1 2 1 2 -1
【样例2输出】
10265
【测试样例】
【数据规模与约定】
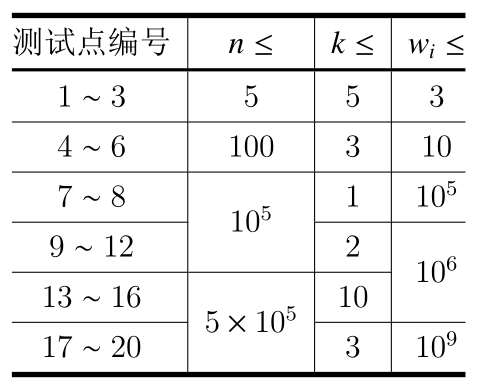
对与所有测试点,保证$1\leq n\leq 5\times 10^5,1\leq k\leq 10,1\leq w_i\leq 10^9,d_i\in\{-1,1\}$。
【来源】
NOIP 2020 Task 4