| 比赛场次 | 505 |
|---|---|
| 比赛名称 | EYOI常规赛 4th |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2022-05-28 18:00:00 |
| 结束时间 | 2022-05-29 00:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | lavey |
| 注释介绍 | seium自虐赛 |
| 题目名称 | 树的重心 |
|---|---|
| 输入输出 | centroid.in/out |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 256 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|
【题目描述】
小简单正在学习离散数学,今天的内容是图论基础,在课上他做了如下两条笔记:
1. 一个大小为 $n$ 的树由 $n$ 个结点与 $n − 1$ 条无向边构成,且满足任意两个结点间有且仅有一条简单路径。在树中删去一个结点及与它关联的边,树将分裂为若干个子树;而在树中删去一条边(保留关联结点,下同),树将分裂为恰好两个子树。
2. 对于一个大小为 $n$ 的树与任意一个树中结点 $c$,称 $c$ 是该树的重心当且仅当在树中删去 $c$ 及与它关联的边后,分裂出的所有子树的大小均不超过 $\lfloor \frac{n}{2} \rfloor$(其中 $\lfloor x \rfloor$ 是下取整函数)。对于包含至少一个结点的树,它的重心只可能有 1 或 2 个。
课后老师给出了一个大小为 $n$ 的树 $S$,树中结点从 $1 \sim n$ 编号。小简单的课后作业是求出 $S$ 单独删去每条边后,分裂出的两个子树的重心编号和之和。即:
$$\sum_{(u,v) \in E} \left( \sum_{1 \leq x \leq n \atop 且 x 号点是 S'_u 的重心} x + \sum_{1 \leq y \leq n \atop 且 y 号点是 S'_v 的重心} y \right)$$
上式中,$E$ 表示树 $S$ 的边集,$(u,v)$ 表示一条连接 $u$ 号点和 $v$ 号点的边。$S'_u$ 与 $S'_v$ 分别表示树 $S$ 删去边 $(u,v)$ 后,$u$ 号点与 $v$ 号点所在的被分裂出的子树。
小简单觉得作业并不简单,只好向你求助,请你教教他。大样例
【输入格式】
本题包含多组测试数据
第一行一个整数 $T$ 表示数据组数。
接下来依次给出每组输入数据,对于每组数据:
第一行一个整数 $n$ 表示树 $S$ 的大小。
接下来 $n − 1$ 行,每行两个以空格分隔的整数 $u_i$,$v_i$,表示树中的一条边 $(u_i,v_i)$。
【输出格式】
共 $T$ 行,每行一个整数,第 $i$ 行的整数表示:第 $i$ 组数据给出的树单独删去每条边后,分裂出的两个子树的重心编号和之和。
【样例输入】
2 5 1 2 2 3 2 4 3 5 7 1 2 1 3 1 4 3 5 3 6 6 7
【样例输出】
32 56
【提示】
对于第一组数据:
删去边 $( 1,2 )$,1 号点所在子树重心编号为 $\{1\}$,2 号点所在子树重心编号为 $\{2,3\}$。
删去边 $( 2,3 )$,2 号点所在子树重心编号为 $\{2\}$,3 号点所在子树重心编号为 $\{3,5\}$。
删去边 $( 2,4 )$,2 号点所在子树重心编号为 $\{2,3\}$,4 号点所在子树重心编号为 $\{4\}$。
删去边 $( 3,5 )$,3 号点所在子树重心编号为 $\{2\}$,5 号点所在子树重心编号为 $\{5\}$。
因此答案为 1 + 2 + 3 + 2 + 3 + 5 + 2 + 3 + 4 + 2 + 5 = 32。
【样例解释】
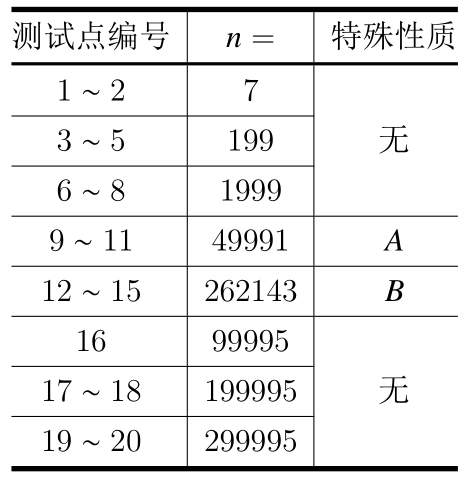
表中特殊性质一栏,两个变量的含义为存在一个 $1 \sim n$ 的排列 $p_i (1 \leq i \leq n)$,使得:
• A:树的形态是一条链。即 $\forall 1 \leq i \lt n$,存在一条边 $(p_i, p_i + 1)$。
• B:树的形态是一个完美二叉树。即 $\forall 1 \leq i \leq \frac{n-1}{2}$ ,存在两条边 $(p_i, p_{2i})$ 与 $(p_i, p_{2i+1})$。
对于所有测试点:$1 \leq T \leq 5 , 1 \leq u_i,v_i \leq n$。保证给出的图是一个树。
【来源】
CSP-S 2019 Day2 Task 3