| 比赛场次 | 624 |
|---|---|
| 比赛名称 | 2024暑假C班集训E |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2024-07-14 08:00:00 |
| 结束时间 | 2024-07-14 12:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | HXF |
| 注释介绍 | 4<1<2,3 |
| 题目名称 | 灾难 |
|---|---|
| 输入输出 | catas.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAA | 0.199 s | 6.00 MiB | 100 |
|
|
AAAAAAAAAA | 0.806 s | 11.21 MiB | 100 |
|
|
TTTATAAAAA | 8.281 s | 4.67 MiB | 60 |
|
|
TTTATAAAAA | 8.412 s | 5.54 MiB | 60 |
|
|
TTTTTAAAAA | 10.246 s | 3.72 MiB | 50 |
|
|
EEEAEWWAAA | 1.159 s | 3.42 MiB | 40 |
|
|
TTTTTTTWWA | 13.751 s | 7.68 MiB | 10 |
|
|
C | 0.000 s | 0.00 MiB | 0 |
|
|
EEEEEEEEEW | 1.980 s | 5.69 MiB | 0 |
|
|
EEEEEEEEEE | 2.325 s | 3.88 MiB | 0 |
【问题描述】
阿米巴是小强的好朋友。
阿米巴和小强在草原上捉蚂蚱。小强突然想,如果蚂蚱被他们捉灭绝了,那么吃蚂蚱的小鸟就会饿死,而捕食小鸟的猛禽也会跟着灭绝,从而引发一系列的生态灾难。
学过生物的阿米巴告诉小强,草原是一个极其稳定的生态系统。如果蚂蚱灭绝了,小鸟照样可以吃别的虫子,所以一个物种的灭绝并不一定会引发重大的灾难。
我们现在从专业一点的角度来看这个问题。我们用一种叫做食物网的有向图来描述生物之间的关系:
一个食物网有 $N$ 个点,代表 $N$ 种生物,如果生物 $x$ 可以吃生物 $y$,那么从 $y$ 向 $x$ 连一个有向边。
这个图没有环。
图中有一些点没有连入边,这些点代表的生物都是生产者,可以通过光合作用来生存; 而有连出边的点代表的都是消费者,它们必须通过吃其他生物来生存。
如果某个消费者的所有食物都灭绝了,它会跟着灭绝。
我们定义一个生物在食物网中的“灾难值”为,如果它突然灭绝,那么会跟着一起灭绝的生物的种数。
举个例子:在一个草场上,生物之间的关系是:
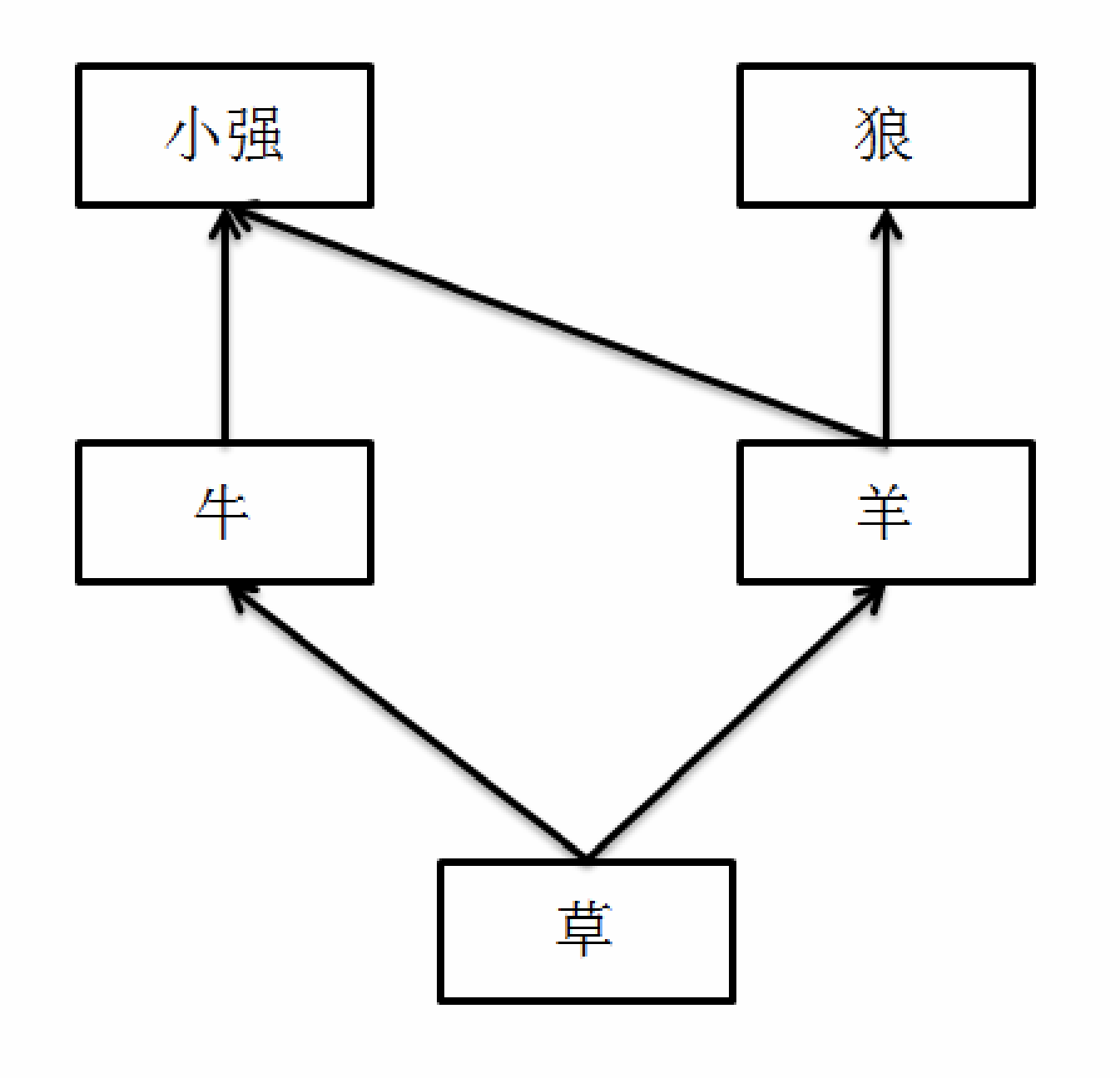
如果小强和阿米巴把草原上所有的羊都给吓死了,那么狼会因为没有食物而灭绝,而小强和阿米巴可以通过吃牛、牛可以通过吃草来生存下去。所以,羊的灾难值是 $1$。但是,如果草突然灭绝,那么整个草原上的 $5$ 种生物都无法幸免,所以,草的灾难值是 $4$。
给定一个食物网,你要求出每个生物的灾难值。
【输入格式】
输入文件第一行是一个正整数 $N$,表示生物的种数。生物从 $1$ 标号到 $N$。
接下来 $N$ 行,每行描述了一个生物可以吃的其他生物的列表,格式为用空格隔开的若干个数字,每个数字表示一种生物的标号,最后一个数字是 $0$ 表示列表的结束。
【输出格式】
输出文件包含 $N$ 行,每行一个整数,表示每个生物的灾难值。
【输入样例1】
5 0 1 0 1 0 2 3 0 2 0
【输出样例1】
4 1 0 0 0
【样例1说明】
样例输入描述了题目描述中举的例子。
【输入输出样例2】
输入输出样例2
【数据规模】
对 $50 \%$ 的数据,$N \leq 10000$;
对 $100 \%$ 的数据,$1 \leq N \leq 65534$;
输入文件的大小不超过 $1M$。保证输入的食物网没有环。