2. 彩色道路

【题目背景】

K 市的市长 老A 成功地改进了该市的道路规划。然而，来自 R 市的一位售货员仍然抱怨道路的颜色不够丰富。老A 的下一个任务就是粉刷一些道路。

【题目描述】

K 市的道路规划可以表示为 $N$ 个十字路口和 $M$ 条道路，第 $i$ 条道路连接第 ui 个十字路口和第 vi 个十字路口。一开始所有道路都是灰色的。老A 想要把一些道路染成红色或者蓝色，满足以下条件：

• 对于每一条灰色道路，假设其连接十字路口 ui 和十字路口 vi，一定存在一条从十字路口 ui 到十字路口 vi 的路径，满足路径上的道路颜色红色和蓝色交替出现，任何道路都不是灰色的。

为了降低城市的支出，老A 希望尽可能少地对道路进行染色。请帮助 K 市设计一个符合要求的染色方案。

【输入格式】

输入的第一行包含两个整数 $N$ 和 $M$（$1\le N,M\le 2\times 10^5$）。

接下来 $M$ 行中的第 $i$ 行包含两个整数 ui 和 vi 表示存在一条连接十字路口 ui 和十字路口 vi 的道路（1≤ui,vi≤N，ui  != vi）。

任意两个十字路口之间至多存在一条道路。

【输出格式】

输出一个长度为 $M$ 的字符串，表示染色的方案。第 $i$ 个字符表示第 $i$ 条道路的颜色，R 表示红色，B 表示蓝色，G 表示灰色（未染色）。

注意你必须在满足条件的情况下最小化染色的道路数目。如果存在多个这样的染色方案，输出任意一个。

【样例输入1】

5 7
1 2
2 4
5 2
4 5
4 3
1 3
1 4

【样例输出1】

BRGBBGG

【样例输入2】

4 2
1 2
3 4

【样例输出2】

BB

【样例说明】

【样例 1 解释】 

十字路口以及有效的道路的示意图如下所示，该方案最小化了染色道路的数量。请注意，每条道路上的颜色显示为 R（红色）、B（蓝色）或 G（灰色）。

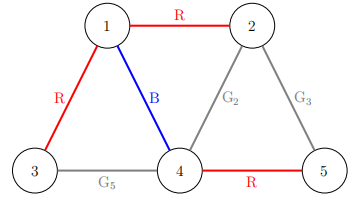
所有为染色的道路都满足条件：

• 第二条路标记为 G2 连接了十字路口 $2$ 和 $4$，路径 $2,1,4$ 上的道路被染上红色、蓝色。
• 第三条路标记为 G3 连接了十字路口 $5$ 和 $2$，路径 $5,4,1,2$ 上的道路被染上红色、蓝色、红色。
• 第五条路标记为 G5 连接了十字路口 $4$ 和 $3$，路径 $4,1,3$ 上的道路被染上蓝色、红色。

【样例 2 解释】

请注意 Kitchener 的道路可能不是连通的。

大样例

【数据规模与约定】

对于所有数据，保证 $1\le N,M\le 2\times 10^5$，1≤ui,vi≤N，ui ≠ vi

【来源】

在此键入。