| 比赛场次 | 549 |
|---|---|
| 比赛名称 | 2022级数学专题练习赛8 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2023-02-06 18:40:00 |
| 结束时间 | 2023-02-06 22:10:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 以赛代练 |
| 题目名称 | 组合数问题 |
|---|---|
| 输入输出 | problem.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试点数 | 20 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAEEEEEEEEEEEEEEE |
3.225 s | 0.00 MiB | 25 |
【题目描述】
众所周知,小葱同学擅长计算,尤其擅长计算组合数。小葱现在希望你计算
$$\left(\sum_{k=0}^nf(k)\times x^k\times C_n^k\right) \mod p$$
的值。其中 $n,x,p$ 为给定的整数,$f(k)$ 为给定的一个 $m$ 次多项式 $f(k)=a_0+a_1k+a_2k^2+\cdots+a_mk^m$。$C_n^k$ 为组合数,其值为 $C_n^k=\frac{n!}{k!(n-k)!}$。
【输入格式】
第一行四个非负整数 $n,x,p,m$。
第二行 $m + 1$ 个整数,分别代表 $a_0,a_1,\cdots,a_m$。
【输出格式】
仅一行一个整数表示答案。
【样例1输入】
5 1 10007 2 0 0 1
【样例1输出】
240
【样例1解释】
$f(0) = 0,f(1) = 1,f(2) = 4,f(3) = 9,f(4) = 16,f(5) = 25$。
$x=1$,故 $x^k$ 恒为 1,乘积中的该项可以忽略。
$C_5^0=1,C_5^1=5,C_5^2=10,C_5^3=10,C_5^4=5,C_5^5=1$。
最终答案为:
$\sum_{k=0}^5f(k)\times C_5^k = 0 × 1 + 1 × 5 + 4 × 10 + 9 × 10 + 16 × 5 + 25 × 1 = 240$
【样例2输入】
996 233 998244353 5 5 4 13 16 20 15
【样例2输出】
869469289
【样例3】
【提示】
评测时请使用 -O2 评测机。
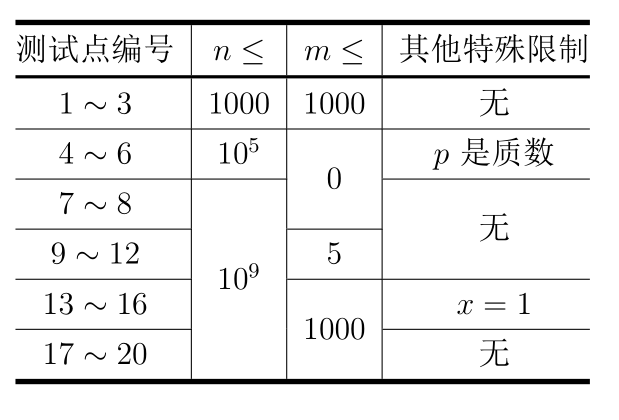
对于所有测试数据:$1 ≤ n,x,p ≤ 10^9,0 ≤ a_i ≤ 10^9 ,0 ≤ m ≤ min(n,1000)$。每个测试点的具体限制见下表:
【来源】
HAOI2020 Day1 Task2