| 比赛场次 | 171 |
|---|---|
| 比赛名称 | 20120919dfs |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2012-09-19 19:00:00 |
| 结束时间 | 2012-09-19 22:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | cqw |
| 注释介绍 |
| 题目名称 | 棋盘分割 |
|---|---|
| 输入输出 | division.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AATTAAAATT | 4.323 s | 3.13 MiB | 60 |
【问题描述】
将一个$8×8$的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将分割过的部分任选一块继续如此分割,这样割了$n-1$次后,连同最后剩下的矩形棋盘共有$n$块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
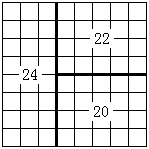
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成 $n$ 块矩形棋盘,并使各矩形棋盘总分的均方差最小。均方差$\sigma=\sqrt{\frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n}}$ ,其中平均值$\bar{x}=\frac{\sum_{i=1}^{n}x_i}{n}$,$x_i$为第 $i$ 块矩形棋盘的分。
请编程对给出的棋盘及$ n $,求出$\sigma$的最小值。
【输入格式】
第 1 行为一个整数 $n(1<n<15)$。
第 2 行至第 9 行每行为 $8$ 个小于 $100$ 的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
【输出格式】
仅一个数,为$\sigma$四舍五入精确到小数点后三位)。
【输入样例】
3 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 3
【输出样例】
1.633