| 比赛场次 | 649 |
|---|---|
| 比赛名称 | 20241129 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2024-11-29 07:30:00 |
| 结束时间 | 2024-11-29 12:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | yuan |
| 注释介绍 | 1122 |
| 题目名称 | 路径覆盖 |
|---|---|
| 输入输出 | lucover.in/out |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAA | 0.316 s | 14.87 MiB | 100 |
|
|
AAAAAAAAAA | 0.438 s | 9.36 MiB | 100 |
|
|
WWWWWWWWWW | 0.315 s | 3.62 MiB | 0 |
|
|
RRRRRRRRRR | 2.015 s | 3.12 MiB | 0 |
【题目背景】
敢问 $NOIP$ 之路在何方?路在脚下。
【题目描述】
有棵 $n$ 个点的无根树,小小想用若干路径覆盖所有边,且保证任意一条边恰被覆盖一次。
“奇数度点数除以 $2$”——小 $A$ 同学脱口而出。既然这题已经被秒了,小小只好重新出一道题。
你可以使用下面 $2$ 种操作来覆盖所有边,且保证任意一条边恰被覆盖一次:
1.选择一条路径 $(u,v)$ ,覆盖路径上的每一条边(前提是路径上所有边都没有被覆盖);
2.选择一个点 $u$ ,覆盖与 $u$ 相连的所有边(前提是与 $u$ 相连的所有边都没有被覆盖);
有 $q$ 次独立询问:每次首先指定一个点 $x$ 进行操作 $2$,求最小化操作次数(即输出覆盖剩下的森林所需的最小操作次数$+1$)。
【输入格式】
第一行输入两个整数 $n,q$。
接下来 $n-1$ 行,每行 $2$ 个整数 $(u,v)$ 代表一条边。
最后一行,包含 $q$ 个整数$x$,代表询问。
【输出格式】
输出 $q$ 行,每行 $1$ 个整数代表答案。
【样例输入1】
5 5 3 1 1 4 4 5 5 2 1 2 3 4 5
【样例输出1】
2 2 2 3 2
【样例输入2】
5 5 1 2 2 3 2 4 1 5 1 2 3 4 5
【样例输出2】
2 2 2 2 2
【样例输入3】
5 5 1 2 1 3 1 4 3 5 1 2 3 4 5
【样例输出3】
2 2 2 2 2
【样例输入4】
5 5 1 2 2 3 2 4 2 5 1 2 3 4 5
【样例输出4】
3 1 3 3 3
【样例5】
点击下载样例5
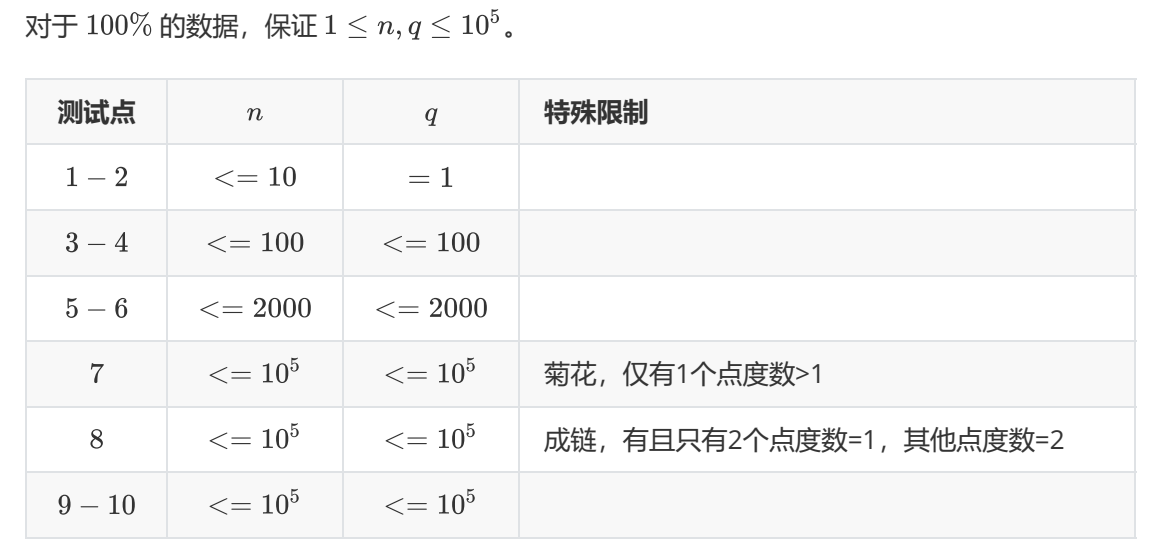
【数据规模与约定】