| 比赛场次 | 619 |
|---|---|
| 比赛名称 | 2024暑假C班集训9 |
| 比赛状态 | 已结束比赛成绩 |
| 开始时间 | 2024-07-09 08:00:00 |
| 结束时间 | 2024-07-09 12:00:00 |
| 开放分组 | 全部用户 |
| 组织者 | HXF |
| 注释介绍 |
| 题目名称 | 天才魔法少女琪露诺爱计数 |
|---|---|
| 输入输出 | cirnoisclever.in/out |
| 时间限制 | 666 ms (0.666 s) |
| 内存限制 | 256 MiB |
| 测试点数 | 10 简单对比 |
| 用户 | 结果 | 时间 | 内存 | 得分 |
|---|---|---|---|---|
|
|
AAAAAAAAAA | 0.019 s | 1.60 MiB | 100 |
|
|
AAAAAAAATT | 2.953 s | 5.81 MiB | 80 |
|
|
AAAAAAAATT | 3.234 s | 16.79 MiB | 80 |
|
|
AAAAWWAAWW | 0.832 s | 3.06 MiB | 60 |
|
|
AAAAWWTTWW | 1.418 s | 2.98 MiB | 40 |
|
|
AAAATTTTTT | 4.125 s | 5.93 MiB | 40 |
|
|
AAWWWWWWWW | 0.003 s | 3.44 MiB | 20 |
|
|
AAWWWWWWWW | 0.008 s | 1.47 MiB | 20 |
|
|
AAWWWWWEEE | 0.547 s | 1.72 MiB | 20 |
|
|
AAWWWWWWTT | 3.030 s | 5.20 MiB | 20 |
|
|
AATTTTTTEE | 4.431 s | 4.89 MiB | 20 |
|
|
AATTTTTTTT | 5.328 s | 5.81 MiB | 20 |
|
|
AWWTWWTTWT | 2.683 s | 3.09 MiB | 10 |
|
|
WWWWWWWWWW | 0.000 s | 0.00 MiB | 0 |
|
|
RRRRRRRRRR | 0.000 s | 0.00 MiB | 0 |
|
|
RRRRRRRRRR | 0.006 s | 11.84 MiB | 0 |
|
|
RRRRRRTTTT | 2.713 s | 6.19 MiB | 0 |
【题目描述】
琪露诺闲来无事,用冰块制造了了$N$个台阶,沿直线依次摆放,编号$1, 2, 3...,⑨, ...N$,分别高$H(1)$, $H(2)$, ... $H(N)$
琪露诺很满意自己的作品,想把自己抓到的青蛙放到台阶上玩,玩法也很简单。 青蛙最开始在第一个台阶上,它只能往前面编号更大的台阶上跳。如果现在在第$k$个台阶上,它至少要跳到第$(k+L)$个台阶上,最多只能跳到第$(k+R)$个台阶上,而且目标台阶现在所在的这个台阶,它们高度的绝对值之差,不能超过$T$。否则青蛙会跳不上去或者摔死。(这时候只有琪露诺给它续它才能复活,而琪露诺是不会给青蛙续的)。
琪露诺想知道青蛙跳到第$N$个,也就是最后一个台阶上,有多少种路线呢?琪露诺是天才魔法少女,但是数数用的是⑨进制,她数出来的结果别人是无法理解的,所以她找你来帮忙了,请你告诉大家,青蛙有有多少条路线可以走呢?告诉大家方案数对998244353取模的结果就可以啦,无法到达的话,方案数自然就是0。
2017.09.28更新:对题目进行一些科学性的说明:
大家都想知道,为什么样例数据1里面,青蛙可以跳过去,原因是这样的,我们进行一个情景模拟:
现在琪露诺抓到的一只青蛙,在高台上准备跳跃:
 然后她跳了起来(我们这里忽略阻力做功,机械能守恒),
然后她跳了起来(我们这里忽略阻力做功,机械能守恒), 跳到了高度比当前高20000的地方(这意味着她的身体可以承受把她自己送到更高的20000高度的高空产生的反冲力)
跳到了高度比当前高20000的地方(这意味着她的身体可以承受把她自己送到更高的20000高度的高空产生的反冲力)
然后再落下 ,即使两个高度为1的高台之间,有一座高度100的高台,也是无法阻挡她跳过去的。但是又有问题了:为什么她落地点所在高台,不能高于她跳跃之前所在高台太多呢?因为跳完一次她会比较累,会休息一会儿,而海拔高度差过大的话,氧气浓度减少的梯度太大,且时间较长,会导致她难受昏厥。那为什么落地点所在高台不能低于她跳跃之前所在高台太多呢?我们做一个定量的计算:
,即使两个高度为1的高台之间,有一座高度100的高台,也是无法阻挡她跳过去的。但是又有问题了:为什么她落地点所在高台,不能高于她跳跃之前所在高台太多呢?因为跳完一次她会比较累,会休息一会儿,而海拔高度差过大的话,氧气浓度减少的梯度太大,且时间较长,会导致她难受昏厥。那为什么落地点所在高台不能低于她跳跃之前所在高台太多呢?我们做一个定量的计算:
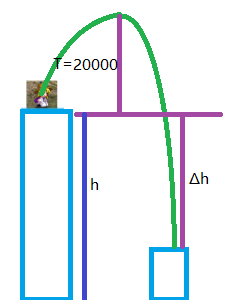
设这只青蛙的质量为$m$从最高点处落到目标高台上的落地点时,在竖直方向上的分速度为$v$
则有$v^2 = 2g(T+\Delta h), v = \sqrt{2g(T+\Delta h)}$,落地时在竖直方向上有动量$p = mv = m\sqrt{2g(T+\Delta h)}$,由于高台质量很大,与青蛙发生碰撞时,我们不妨看作所有动量都转化为了青蛙受到的冲量$I$,假设青蛙落到高台上受到竖直向上的力为$F$,作用时间为$t$,那么就有$I = Ft$,得$F = mv = \frac{m\sqrt{2g(T+\Delta h)}}{t}$,根据相关人生经验可知,这个$t$是很小的(不妨设$t = 0.05s$),而$I$是很大的。我们之前提到过,这只青蛙能够承受将她送到更高的$20000$高度的高空产生的反冲力,可以算出来,这个反冲力的,青蛙跳出去一直到最高点的过程中,在竖直方向上有跳跃需要的竖直方向初速度$v_{0}^2 = 2gT, v_{0} = \sqrt{2gT}$,同理根据动量守恒我们也可以算出跳跃需要的力$F_{0} = \frac{I_{0}}{t} = \frac{mv_{0}}{t} = \frac{m\sqrt{2gT}}{t} \ll F$,也就是说,在目标高台远远低于当前所在高台的时候,虽然这只青蛙能够承受跳跃出去产生的反冲力,但是会因为无法承受落地时收到的力的冲击而被摔死,而琪露诺并不会给她续使得她复活,所以青蛙为了生命安全是不能跳到跟当前比太低的高台上的。
【输入格式】
第一行4个正整数,$N, L, R, T$,含义如题面所示
接下来第二行,$N$个正整数,依次表示这$N$个高台的高度。
【输出格式】
青蛙跳到最后一个高台上面的方案数对998244353取模的结果。
【样例】
input1
3 2 2 0
1 100 1
output1
1
解释1
只有一种方案,从第1个高台直接跳到第3个高台。第二个高台虽然高100但是并不会影响青蛙跳过它,因为这些青蛙是经过早苗开光的
input2
5 1 2 5
1 2 3 4 5
output2
5
解释2:
#5条路线分别是(数字代表高台的编号):
1-2-3-4-5
1-2-3-5
1-2-4-5
1-3-4-5
1-3-5
input3
20 1 4 12
1 2 3 4 5 6 7 100 9 10 11 12 11 100 1 2 3 4 5 6
output3
27680
解释3
良心大♂样例
【数据范围】
对于20%的数据:$N \leq 20$,
对于另外20%的数据:$N \leq 10000, R-L+1 \leq 1000$
对于另外20%的数据:$N \leq 20000,T = 0$
对于另外20%的数据:$N \leq 20000$。
对于100%的数据:$N \leq 100000, 1 \leq R-L+1 \leq N,1 \leq H(i) \leq 10000, T \leq 10000$
【来源】
by sxysxy。