| 题目名称 | 283. [NOI 1999]钉子和小球 |
|---|---|
| 输入输出 | ball.in/out |
| 难度等级 | ★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 5 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:38, 提交:112, 通过率:33.93% | ||||
|
|
100 | 0.000 s | 0.00 MiB | C++ |
|
|
100 | 0.001 s | 0.32 MiB | C++ |
|
|
100 | 0.001 s | 0.32 MiB | C++ |
|
|
100 | 0.001 s | 0.34 MiB | C++ |
|
|
100 | 0.001 s | 0.37 MiB | C++ |
|
|
100 | 0.002 s | 0.35 MiB | C++ |
|
|
100 | 0.002 s | 0.36 MiB | C++ |
|
|
100 | 0.002 s | 0.38 MiB | C++ |
|
|
100 | 0.002 s | 0.44 MiB | C++ |
|
|
100 | 0.002 s | 0.51 MiB | C++ |
| 本题关联比赛 | |||
| 防止浮躁的小练习 | |||
| 关于 钉子和小球 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
= =快速幂要开long long
| ||||
|
这个高精实在恶心到我了- -。。
| ||||
|
分数分子分母增涨速度快如狗
| ||||
|
这样可以无视精度问题。。。计算几何也可以用解析几何解了。。。
2013-05-05 14:56
2楼
| ||||
|
代码里包含一个分数类,功能:约分,输出,重载了四则运算(包括分数间,分数与整数间)和比较大小的运算符
(我才不会告诉你这是前几天写的……) | ||||
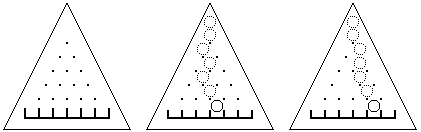
有一个三角形木板,竖直立放,上面钉着n(n+1)/2颗钉子,还有(n+1)个格子(当n=5时如图1)。每颗钉子和周围的钉子的距离都等于d,每个格子的宽度也都等于d,且除了最左端和最右端的格子外每个格子都正对着最下面一排钉子的间隙。
让一个直径略小于d的小球中心正对着最上面的钉子在板上自由滚落,小球每碰到一个钉子都可能落向左边或右边(概率各1/2),且球的中心还会正对着下一颗将要碰上的钉子。例如图2就是小球一条可能的路径。
我们知道小球落在第i个格子中的概率pi= ![]() ,其中i为格子的编号,从左至右依次为0,1,...,n。
,其中i为格子的编号,从左至右依次为0,1,...,n。
现在的问题是计算拔掉某些钉子后,小球落在编号为m的格子中的概率pm。假定最下面一排钉子不会被拔掉。例如图3是某些钉子被拔掉后小球一条可能的路径。
输入
第1行为整数n(2<=n<=50)和m(0<=m<=n)。以下n行依次为木板上从上至下n行钉子的信息,每行中‘*’表示钉子还在,‘.’表示钉子被拔去,注意在这n行中空格符可能出现在任何位置。
输出
仅一行,是一个既约分数(0写成0/1),为小球落在编号为m的格子中的概pm。既约分数的定义:A/B是既约分数,当且仅当A、B为正整数且A和B没有大于1的公因子。
样例输入
5 2
*
* .
* * *
* . * *
* * * * *
样例输出
7/16