| 题目名称 | 592. [NOIP 2007]树网的核(加强版) |
|---|---|
| 输入输出 | core.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:10, 提交:27, 通过率:37.04% | ||||
|
|
100 | 0.613 s | 12.40 MiB | C++ |
|
|
100 | 0.697 s | 42.73 MiB | C++ |
|
|
100 | 0.773 s | 44.18 MiB | C++ |
|
|
100 | 0.837 s | 57.22 MiB | C++ |
|
|
100 | 1.069 s | 17.68 MiB | C++ |
|
|
100 | 1.222 s | 13.97 MiB | C++ |
|
|
100 | 1.530 s | 25.70 MiB | C++ |
|
|
100 | 1.739 s | 32.51 MiB | C++ |
|
|
100 | 1.871 s | 53.48 MiB | C++ |
|
|
100 | 1.880 s | 32.50 MiB | C++ |
| 关于 树网的核(加强版) 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
二分 ?数组开小不过,数组开大也不过是吧$qwq$?
为啥嘞?┭┮﹏┭┮ | ||||
【问题描述】
设T=(V,E,W)是一个无圈且连通的无向图(也称为无根树),每条边带有正整数的权,我们称T为树网(treenetwork),其中v,E分别表示结点与边的集合,W表示各边长度的集合,并设T有n个结点。
路径:树网中任何两结点a,b都存在唯一的一条简单路径,用d(a,b)表示以a,b为端点的路径的长度,它是该路径上各边长度之和。我们称d(a,b)为a,b两结点问的距离。
一点v到一条路径p的距离为该点与p上的最近的结点的距离:d(v,P)=min{d(v,u),u为路径P上的结点)。
树网的直径:树网中最长的路径称为树网的直径。对于给定的树网T,直径不一定是唯一的,但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该点为树网的中心。
偏心距ECC(F):树网T中距路径F最远的结点到路径F的距离,即 ECC(F)=max{d(v,F),V∈V}。
任务:对于给定的树网T=(V,E,W)和非负整数s,求一个路径F,它是某直径上的一段路径(该路径两端均为树网中的结点),其长度不超过s(可以等于s),使偏心距ECC(F)最小。我们称这个路径为树网T=(V,E,W)的核(Core)。必要时,F可以退化为某个结点。一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。
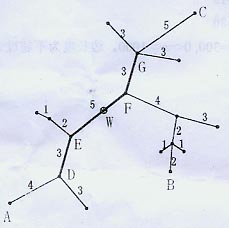
下面的图给出了树网的一个实例。图中,A-B与A-C是两条直径,长度均为20。点W是树网的中心,EF边的长度为5。如果指定s=11,则树网的核为路径DEFG(也可以取为路径DEF),偏心距为8。如果指定s=O(或s=1、s=2),则树网的核为结点F,偏心距为12。
【输入格式】
输入包含n行:
第1行,两个正整数n和S,中间用一个空格隔开。其中n为树网结点的个数,s为树网的核的长度的上界。设结点编号依次为1,2,…,n。
从第2行到第n行,每行给出3个用空格隔开的正整数,依次表示每一条边的两个端点编号和长度。例如,“2 4 7”表示连接结点2与4的边的长度为7。
所给的数据都是正确的,不必检验。
【输出格式】
输出只有一个非负整数,为指定意义下的最小偏心距。
【输入样例1】
5 2 1 2 5 2 3 2 2 4 4 2 5 3
【输出样例1】
5
【输入样例2】
8 6 1 3 2 2 3 2 3 4 6 4 5 3 4 6 4 4 7 2 7 8 3
【输出样例2】
5
【数据范围与约定】
20%的数据满足:5<=n<=15
35%的数据满足:5<=n<=80
50%的数据满足:5<=n<=300,0<=s<=1000,边长度为不超过1000的正整数。
100%的数据满足:5<=n<=5*10^5,0<=s<=2*10^9。