| 题目名称 | 103. [NOIP 2002]矩形覆盖 |
|---|---|
| 输入输出 | jxfg.in/out |
| 难度等级 | ★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 7 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:24, 提交:346, 通过率:6.94% | ||||
|
|
100 | 0.009 s | 0.32 MiB | C++ |
|
|
100 | 0.011 s | 0.04 MiB | C++ |
|
|
100 | 0.038 s | 0.31 MiB | C++ |
|
|
100 | 0.040 s | 0.31 MiB | C++ |
|
|
100 | 0.047 s | 0.31 MiB | C++ |
|
|
100 | 0.052 s | 0.29 MiB | C++ |
|
|
100 | 0.055 s | 0.29 MiB | C++ |
|
|
100 | 0.060 s | 0.82 MiB | C++ |
|
|
100 | 0.079 s | 0.82 MiB | C++ |
|
|
100 | 0.086 s | 0.04 MiB | C++ |
| 本题关联比赛 | |||
| 201712练习 | |||
| EYOI与SBOI开学欢乐赛8th | |||
| 2024暑假C班集训9 | |||
| 关于 矩形覆盖 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
数据已修复 2017/9/4
2017-09-04 17:49
16楼
| ||||
|
数据咋回事,倒数第二个改一下
2017-08-10 18:18
15楼
| ||||
|
回复 @liu_runda :
666666666666666666666666666666666666666666666666666
2017-07-02 21:14
14楼
| ||||
|
这题数据有毒。。。。
| ||||
|
倒数第二组的数据是错的,答案应当为124850而非139108,可行方案为
42 16 391 185 94 296 374 359 7 426 389 496 427 11 484 388 即: 矩形1:左下角(42,16)右上角(391,185) 矩形2:左下角(94,296)右上角(374,359) 矩形3:左下角(7,426 )右上角(389, 496) 矩形4:左下角(427,11)右上角 (484,388) 可以验证,这组方案是合法的。
2016-10-23 17:56
12楼
| ||||
|
| ||||
|
倒数第二个点过不了。。很奇怪的说
| ||||
|
将点按x为第一关键字,y为第二关键字,递增排序。f[i][x1][x2]表示 由点 x1到点 x2范围之内分成 i 个矩形所用的最少面积。这样应该没问题。
| ||||
|
偶,不对,这样好像k=4的时候有反例,还是搜索吧!
2014-11-05 16:03
8楼
| ||||
|
回复 @HouJikan :
x,y两遍还是会有问题的- -可以卡掉 例如这个数据: 8 4 0 0 10 1 8 10000 9 10001 1000 3 1001 4 10000 2 10001 7 显然最优解释是1,2一组,3,4一组,5,6一组,7,8一组 最优解为:17 而你的代码显然不能处理- -事实上也是这样,你跑出来是10000+ - -
2014-10-15 20:14
7楼
| ||||
【题目描述】
在平面上有 $n$ 个点,每个点用一对整数坐标表示。例如:当 $n=4$ 时,$4$ 个点的坐标分另为:$p_1(1,1),p_2(2,2),p_3(3,6),p_4(0,7)$,见图一。
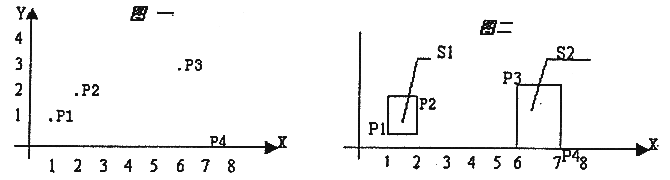
这些点可以用 $k$ 个矩形全部覆盖,矩形的边平行于坐标轴。当 $k=2$ 时,可用如图二的两个矩形 $s_l,s_2$ 覆盖,$s_1,s_2$ 面积和为 $4$。问题是当 $n$ 个点坐标和 $k$ 给出后,怎样才能使得覆盖所有点的 $k$ 个矩形的面积之和为最小呢。
约定:
覆盖一个点的矩形面积为 $0$;
覆盖平行于坐标轴直线上点的矩形面积也为 $0$;
各个矩形必须完全分开(边线与顶点也都不能重合)。
【输入格式】
$n$ $k$
$x_l$ $y_1$
$x_2$ $y_2$
... ...
$x_n$ $y_n$
【输出格式】
一个整数,即满足条件的最小的矩形面积之和。
【输入样例1】
4 2 1 1 2 2 3 6 0 7
【输出样例1】
4
【输入/输出样例2】
输入输出样例2
【数据规模与约定】
对于 $70 \%$ 的数据, 保证 $n \leq 15$;
对于 $100 \%$ 的数据,保证 $n \leq 50,1 \leq k \leq 4,0 \leq x_i,y_i \leq 500$;