| 题目名称 | 411. [NOI 2009]管道取珠 |
|---|---|
| 输入输出 | ballb.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 9 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:81, 提交:200, 通过率:40.5% | ||||
|
|
100 | 0.100 s | 6.49 MiB | C++ |
|
|
100 | 0.105 s | 0.77 MiB | C++ |
|
|
100 | 0.110 s | 5.79 MiB | C++ |
|
|
100 | 0.194 s | 2.26 MiB | C++ |
|
|
100 | 0.266 s | 491.60 MiB | C++ |
|
|
100 | 0.274 s | 2.23 MiB | C++ |
|
|
100 | 0.294 s | 2.05 MiB | C++ |
|
|
100 | 0.546 s | 2.27 MiB | C++ |
|
|
100 | 0.563 s | 2.26 MiB | C++ |
|
|
100 | 0.563 s | 482.89 MiB | C++ |
| 本题关联比赛 | |||
| 2022级DP专题练习赛1 | |||
| 关于 管道取珠 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
卡过了
| ||||
|
string真慢。。。
2013-12-18 16:14
4楼
| ||||
|
orz
2013-06-20 13:00
3楼
| ||||
|
以解决
2013-06-20 09:24
2楼
| ||||
|
注意,题目中的公式未显示,具体看 bzoj
http://www.lydsy.com/JudgeOnline/problem.php?id=1566
2013-06-18 09:38
1楼
| ||||
【题目描述】
管道取珠是小 $X$ 很喜欢的一款游戏。在本题中,我们将考虑该游戏的一个简单改版。游戏画面如图 $1$ 所示:
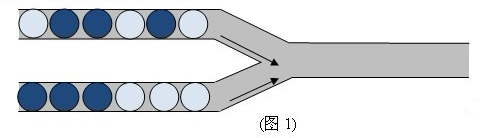
游戏初始时,左侧上下两个管道分别有一定数量的小球(有深色球和浅色球两种类型),而右侧输出管道为空。每一次操作,可以从左侧选择一个管道,并将该管道中最右侧的球推入右边输出管道。
例如:我们首先从下管道中移一个球到输出管道中,将得到图 $2$ 所示的情况。
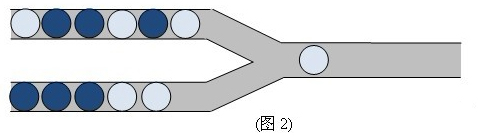
假设上管道中有 $n$ 个球, 下管道中有 $m$ 个球,则整个游戏过程需要进行 $n+m$ 次操作,即将所有左侧管道中的球移入输出管道。最终 $n+m$ 个球在输出管道中从右到左形成输出序列。
爱好数学的小 $X$ 知道,他共有 $\left( \begin{array}{c} n+m \\ m \end{array} \right)$ 种不同的操作方式,而不同的操作方式可能导致相同的输出序列。举个例子,对于图 $3$ 所示的游戏情形:
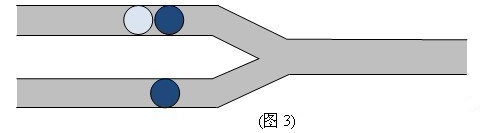
我们用 $A$ 表示浅色球,$B$ 表示深色球。并设移动上管道右侧球的操作为 $U$,移动下管道右侧球的操作为 $D$,则共有 $\left( \begin{array}{c} 2+1 \\ 1 \end{array} \right)$ 种不同的操作方式,分别为 $UUD$,$UDU$,$DUU$;最终在输出管道中形成的输出序列(从右到左)分别为 $BAB$,$BBA$,$BBA$。可以发现后两种操作方式将得到同样的输出序列。
假设最终可能产生的不同种类的输出序列共有 $K$ 种,其中:第 $i$ 种输出序列的产生方式(即不同的操作方式数目)有 $a_i$ 个。聪明的小 $X$ 早已知道,
$\sum a_i = \left( \begin{array}{c} n+m \\ m \end{array} \right)$
因此,小 $X$ 希望计算得到:
$\sum a_i^2$
你能帮助他计算这个值么?由于这个值可能很大,因此只需要输出该值对 $1024523$ 取模后的结果。
【输入格式】
输入文件中的第一行为两个整数 $n,m$,分别表示上下两个管道中球的数目。
第二行中为一个长度为 $n$ 的字符串,表示上管道中从左到右球的类型。其中:$A$ 表示浅色球,$B$ 表示深色球。
第三行中为一个长度为 $m$ 的字符串,表示下管道中从左到右球的类型。
保证两个字符串都只包含 $A,B$ 两个字母。
【输出格式】
输出一个整数,即为 $\sum a_i^2$ 对 $1024523$ 取模的结果。
【样例1输入】
2 1 AB B
【样例1输出】
5
【样例1说明】
样例 $1$ 对应图 $3$。
共有两种不同的输出序列形式,序列 $BAB$ 有 $1$ 种产生方式,而序列 $BBA$ 有 $2$ 种产生方式,因此答案为 $5$。
【样例2输入输出】
点击下载样例2
【数据规模与约定】
对于 $30\%$ 的数据,满足 $m,n \leq 12$;
对于 $100\%$ 的数据,满足 $1 \leq m,n \leq 500$。
【来源】
NOI 2009