| 题目名称 | 4189. Minimum Cost Roads |
|---|---|
| 输入输出 | Roads.in/out |
| 难度等级 | ★★ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:4, 提交:12, 通过率:33.33% | ||||
|
|
100 | 0.427 s | 3.78 MiB | C++ |
|
|
100 | 0.469 s | 3.82 MiB | C++ |
|
|
100 | 0.505 s | 3.88 MiB | C++ |
|
|
100 | 0.686 s | 3.90 MiB | C++ |
|
|
10 | 0.061 s | 3.71 MiB | C++ |
|
|
10 | 0.448 s | 3.86 MiB | C++ |
|
|
10 | 0.458 s | 3.86 MiB | C++ |
|
|
10 | 0.623 s | 3.85 MiB | C++ |
|
|
0 | 0.027 s | 3.71 MiB | C++ |
|
|
0 | 1.360 s | 3.25 MiB | C++ |
| 本题关联比赛 | |||
| csp2025模拟练习3 | |||
| 关于 Minimum Cost Roads 的近10条评论(全部评论) |
|---|
【题目描述】
作为新当选的基奇纳市市长,Alanna 的首要任务是改善城市的道路规划。
基奇纳当前的道路规划可以表示为 $N$ 个交叉路口和 $M$ 条道路的集合,其中第 $i$ 条道路的长度为 $l_i$ 米,每年维护费用为 $c_i$ 美元,并连接交叉路口 $u_i$ 和 $v_i$。为了制定计划,Alanna 必须选择保留和维护的 $M$ 条道路的一个子集,该计划的费用是该子集中所有道路的维护费用之和。
为了降低城市的年度支出,Alanna 希望将计划的费用最小化。然而,城市还要求她最小化交叉路口之间的旅行距离,并拒绝任何不符合这些规则的计划。正式地,对于任何交叉路口对 $(i, j)$,如果在现有道路规划中存在从 $i$ 到 $j$ 的路径,且路径长度为 $l$ 米,则 Alanna 的计划中也必须包含一条长度不超过 $l$ 米的路径。
【输入格式】
第一行包含整数 $N$ 和 $M$。
接下来的 $M$ 行中的每一行包含整数 $u_i, v_i, l_i$ 和 $c_i$,表示当前存在一条从交叉路口 $u_i$ 到交叉路口 $v_i$ 的道路,长度为 $l_i$,费用为 $c_i$($1 \leq u_i, v_i \leq N, u_i \neq v_i$)。
【输出格式】
输出一个整数,表示满足要求的道路规划的最小可能费用。
【样例输入1】
5 7 1 2 15 1 2 4 9 9 5 2 5 6 4 5 4 4 4 3 3 7 1 3 2 7 1 4 2 1
【样例输出1】
25
【样例1说明】
样例输入的输出解释:
这是交叉路口的图示,以及一个具有最小费用的有效道路规划。
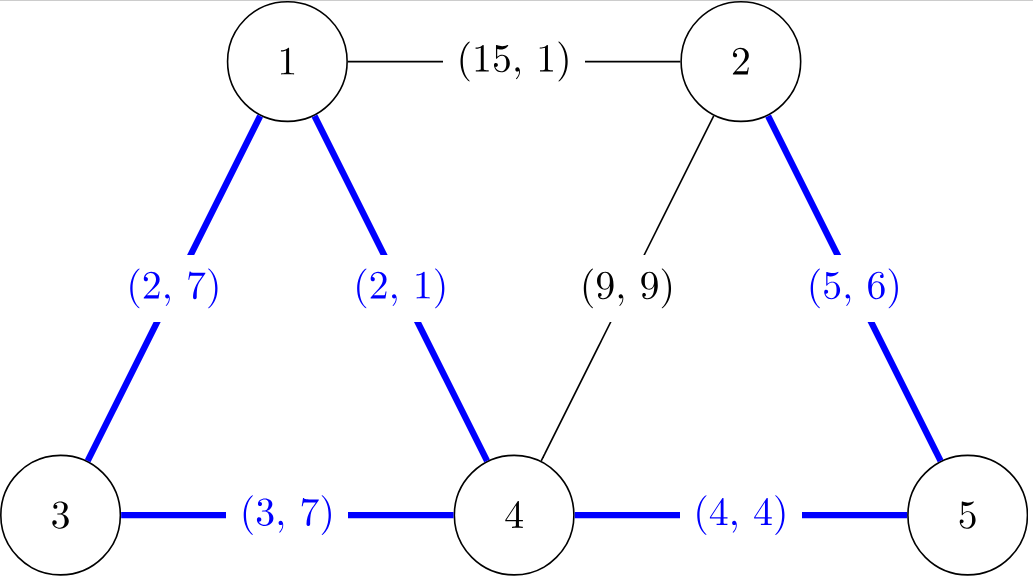
每条边都标有一个对 $(l, c)$,表示其长度为 $l$ 米,费用为 $c$ 美元。
此外,计划中的道路用蓝色突出显示,总费用为 $7 + 1 + 6 + 7 + 4 = 25$。
可以证明,我们无法创建一个更便宜且符合城市要求的计划。
【样例输入输出2】
点击下载大样例
【数据规模与约定】
$20\%$ 的数据保证 $1\leq N \leq 2000$,$1\leq M \leq 2000$,$l_i = 0$,$1\leq c_i \leq 10^9$。
$40\%$ 数据保证 $1\leq N\leq 2000$,$1\leq M \leq 2000$,$1\leq l_i \leq 10^9$,$1\leq c_i \leq 10^9$,且在任何一对十字路口之间最多只有一条路。
$40\%$ 数据保证 $1\leq N\leq 2000$,$1\leq M \leq 2000$,$0\leq l_i \leq 10^9$,$1\leq c_i \leq 10^9$。
【来源】
CCC 2023 S4