| 题目名称 | 3781. [CSP 2022S]假期计划 |
|---|---|
| 输入输出 | holiday.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:20, 提交:83, 通过率:24.1% | ||||
|
|
100 | 0.781 s | 3.00 MiB | C++ |
|
|
100 | 1.041 s | 16.64 MiB | C++ |
|
|
100 | 1.263 s | 1.94 MiB | C++ |
|
|
100 | 1.275 s | 15.94 MiB | C++ |
|
|
100 | 1.496 s | 6.46 MiB | C++ |
|
|
100 | 1.511 s | 29.86 MiB | C++ |
|
|
100 | 1.593 s | 6.12 MiB | C++ |
|
|
100 | 1.611 s | 6.63 MiB | C++ |
|
|
100 | 1.880 s | 53.70 MiB | C++ |
|
|
100 | 1.892 s | 53.69 MiB | C++ |
| 本题关联比赛 | |||
| CSP2022提高组 | |||
| 20250527CSP-S模拟 | |||
| 关于 假期计划 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
挑战最易懂代码
| ||||
|
半天发现没压缩的记忆化搜索和爆搜一个复杂度,绷不住了
2023-07-25 15:11
2楼
| ||||
|
图论专场
 | ||||
【题目描述】
小熊的地图上有 $n$ 个点,其中编号为 $1$ 的是它的家、编号为 $2, 3, \ldots, n$ 的都是景点。部分点对之间有双向直达的公交线路。如果点 $x$ 与 $z_1$、$z_1$ 与 $z_2$、……、$z_{k - 1}$ 与 $z_k$、$z_k$ 与 $y$ 之间均有直达的线路,那么我们称 $x$ 与 $y$ 之间的行程可转车 $k$ 次通达;特别地,如果点 $x$ 与 $y$ 之间有直达的线路,则称可转车 $0$ 次通达。
很快就要放假了,小熊计划从家出发去 $4$ 个不同的景点游玩,完成 $5$ 段行程后回家:家 $\to$ 景点 $A$ $\to$ 景点 $B$ $\to$ 景点 $C$ $\to$ 景点 $D$ $\to$ 家且每段行程最多转车 $k$ 次。转车时经过的点没有任何限制,既可以是家、也可以是景点,还可以重复经过相同的点。例如,在景点 $A$ $\to$ 景点 $B$ 的这段行程中,转车时经过的点可以是家、也可以是景点 $C$,还可以是景点 $D$ $\to$ 家这段行程转车时经过的点。
假设每个景点都有一个分数,请帮小熊规划一个行程,使得小熊访问的四个不同景点的分数之和最大。
【输入格式】
第一行包含三个正整数$n,m,k$,分别表示地图上点的个数、双向直达的点对数量、每段行程最多的转车次数。
第二行包含$n-1$个正整数,分别表示编号为$2,3,\cdots,n$的景点的分数。
接下来$m$行,每行包含两个正整数$x,y$,表示点$x$和$y$之间有道路直接相连,保证$1\leq x,y\leq n$,且没有重边,自环。
【输出格式】
输出一个正整数,表示小熊经过的 个不同景点的分数之和的最大值。
【样例1输入】
8 8 1 9 7 1 8 2 3 6 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 1
【样例1输出】
27
【样例1解释】
当计划的行程为 $1 \to 2 \to 3 \to 5 \to 7 \to 1$ 时,$4$ 个景点的分数之和为 $9 + 7 + 8 + 3 = 27$,可以证明其为最大值。
行程 $1 \to 3 \to 5 \to 7 \to 8 \to 1$ 的景点分数之和为 $24$、行程 $1 \to 3 \to 2 \to 8 \to 7 \to 1$ 的景点分数之和为 $25$。它们都符合要求,但分数之和不是最大的。
行程 $1 \to 2 \to 3 \to 5 \to 8 \to 1$ 的景点分数之和为 $30$,但其中 $5 \to 8$ 至少需要转车 $2$ 次,因此不符合最多转车 $k = 1$ 次的要求。
行程 $1 \to 2 \to 3 \to 2 \to 3 \to 1$ 的景点分数之和为 $32$,但游玩的并非 $4$ 个不同的景点,因此也不符合要求。
【样例2输入】
7 9 0 1 1 1 2 3 4 1 2 2 3 3 4 1 5 1 6 1 7 5 4 6 4 7 4
【样例2输出】
7
【样例下载】
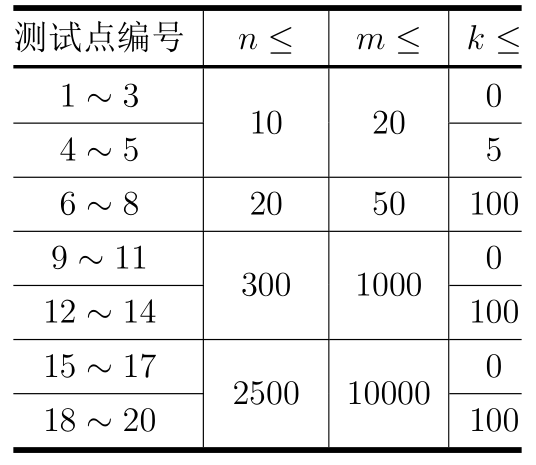
【数据规模与约定】
对于所有数据,保证$5\leq n\leq 2500,1\leq m\leq 10000,0\leq k\leq 100$,所有景点的分数$1\leq s_i\leq 10^{18}$。保证至少存在一组符合要求的行程。
【来源】
CSP 2022提高组 Task1