| 题目名称 | 3307. [Sekai CTF 2025] Nokotans_Guidance |
|---|---|
| 输入输出 | guidance.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:1, 通过率:100% | ||||
|
|
100 | 7.534 s | 160.83 MiB | C++ |
| 关于 Nokotans_Guidance 的近10条评论(全部评论) |
|---|
3307. [Sekai CTF 2025] Nokotans_Guidance
★★☆ 输入文件:guidance.in
输出文件:guidance.out
简单对比时间限制:3 s 内存限制:256 MiB
【题目背景】
好久没回COGS了,前两天打CTF看到了算法题,甚是怀念,搬一道有意思的题给大家写着玩。
题目作者:null_awe

【题目描述】
Nokotan 的世界被转化成了一个 三角图(triangle graph),它包含 $n$ 个节点($3 \leq n \leq 1.5 \times 10^5$)!三角图的构造方式如下:
1. 先从 3 个节点(1, 2, 3)构成的完全图开始。
2. 对于编号从 4 到 $n$ 的每一个新节点,选择现有图中一条相邻的边 $(u, v)$,并将新节点连接到这两个节点 $u$ 和 $v$。
Nokotan 对这片土地极为熟悉而自豪。现在有 $q$ 只鹿($1 \leq q \leq 1.5 \times 10^5$)想要请教 Nokotan 的智慧(大嘘)。第 $i$ 只鹿提出一个查询,给出两个整数 $s_i$ 和 $t_i$,它想知道从节点 $s_i$ 到节点 $t_i$ 的 最短距离。
但 Nokotan 面对这么多问题感到有些不堪重负!请你帮助她!
【输入格式】
第一行包含一个整数 $n$,表示三角图的大小。
接下来 $n - 3$ 行,每行包含两个整数 $u_i, v_i$(对应第 $i$ 个节点,$i$ 范围为 4 到 $n$),表示该新节点连接到的两个相邻节点。
接下来一行包含一个整数 $q$,表示查询的数量。* 接下来 $q$ 行,每行包含两个整数 $s_i, t_i$,表示查询的两个节点。
【输出格式】
对每个查询 $i$,输出从 $s_i$ 到 $t_i$ 的最短距离。
【样例输入】
7 1 2 2 4 3 1 4 2 5 1 5 2 6 3 6 3 7 6 7
【样例输出】
2 2 1 2 3
【样例解释】
根据示例输入构建出的三角图如下所示。
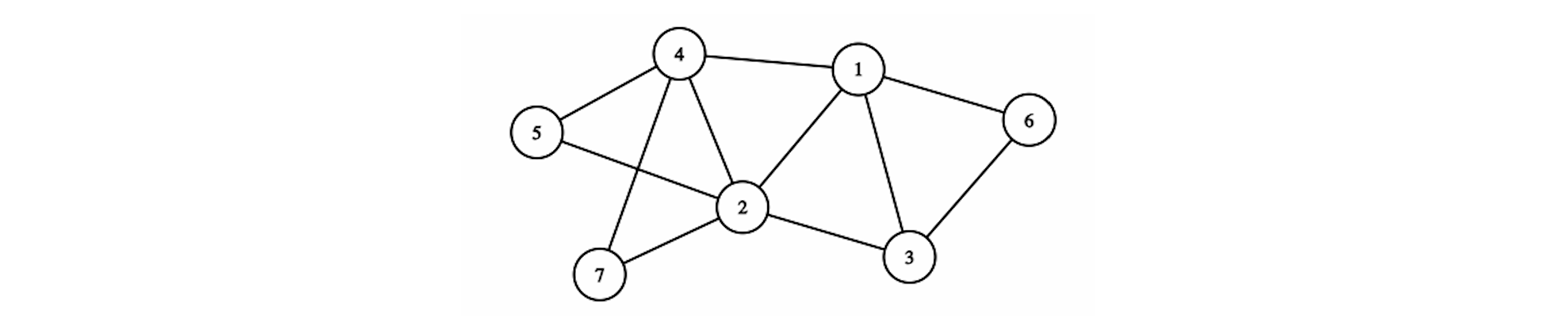
查看每个查询中的节点对,可以确定它们之间的最短距离与示例输出完全一致。
【数据规模与约定】
这道题本来是 XCPC 的评测机制,对OIer可能没那么友好。
为了符合学弟们的 CSP/NOIP 的训练需要,我手搓了一些特殊数据给大家骗,具体描述如下:

【来源】
Project Sekai CTF 2025 PPC 方向,Github链接:nokotans-guidance