| 题目名称 | 4193. [CSP-J 2025 T2]座位 |
|---|---|
| 输入输出 | seat.in/out |
| 难度等级 | ★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:20, 提交:54, 通过率:37.04% | ||||
|
|
100 | 0.052 s | 3.68 MiB | C++ |
|
|
100 | 0.053 s | 3.68 MiB | C++ |
|
|
100 | 0.053 s | 3.71 MiB | C++ |
|
|
100 | 0.054 s | 3.69 MiB | C++ |
|
|
100 | 0.054 s | 3.70 MiB | C++ |
|
|
100 | 0.054 s | 3.71 MiB | C++ |
|
|
100 | 0.054 s | 3.71 MiB | C++ |
|
|
100 | 0.054 s | 3.87 MiB | C++ |
|
|
100 | 0.055 s | 3.67 MiB | C++ |
|
|
100 | 0.055 s | 3.69 MiB | C++ |
| 关于 座位 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
数据量很小,所以数学不是刚需,考场上写的数学,lemon上100
2025-11-02 16:24
1楼
| ||||
【题目描述】
CSP-J 2025 第二轮正在进行。小 R 所在的考场共有 $n \times m$ 名考生,其中所有考生的 CSP-J 2025 第一轮成绩互不相同。所有 $n \times m$ 名考生将按照 CSP-J 2025 第一轮的成绩,由高到低蛇形分配座位,排列成 $n$ 行 $m$ 列。具体地,设小 R 所在的考场的所有考生的成绩从高到低分别为 $s_1 > s_2 > \dots > s_{n \times m}$,则成绩为 $s_1$ 的考生的座位为第 1 列第 $1$ 行,成绩为 $s_2$ 的考生的座位为第 $1$ 列第 $2$ 行,$\dots$,成绩为 $s_n$ 的考生的座位为第 $1$ 列第 $n$ 行,成绩为 $s_{n+1}$ 的考生的座位为第 $2$ 列第 $n$ 行,$\dots$,成绩为 $s_{2n}$ 的考生的座位为第 $2$ 列第 $1$ 行,成绩为 $s_{2n+1}$ 的考生的座位为第 $3$ 列第 $1$ 行,以此类推。
例如,若 $n = 4, m = 5$,则所有 $4 \times 5 = 20$ 名考生将按照 CSP-J 2025 第一轮成绩从高到低的顺序,根据下图中的箭头顺序分配座位。
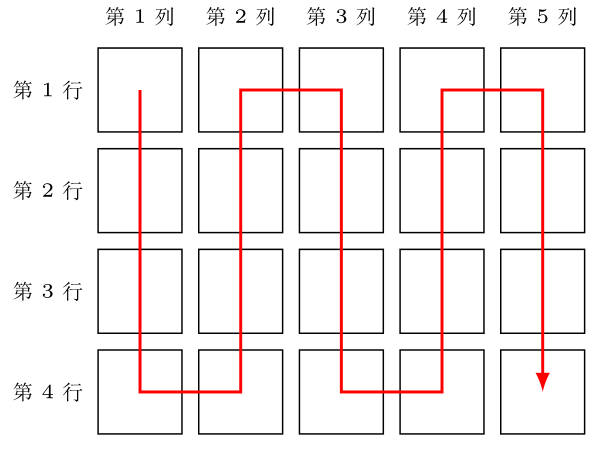
给定小 R 所在的考场座位的行数 $n$ 与列数 $m$,以及小 R 所在的考场的所有考生 CSP-J 2025 第一轮的成绩 $a_1, a_2, \dots, a_{n \times m}$,其中 $a_1$ 为小 R CSP-J 2025 第一轮的成绩,你需要帮助小 R 求出,他的座位为第几列第几行。
【输入格式】
输入的第一行包含两个正整数 $n, m$,分别表示小 R 所在的考场座位的行数与列数。
输入的第二行包含 $n \times m$ 个正整数 $a_1, a_2, \dots, a_{n \times m}$,分别表示小 R 所在的考场的所有考生 CSP-J 2025 第一轮的成绩,其中 $a_1$ 为小 R CSP-J 2025 第一轮的成绩。
【输出格式】
输出一行两个正整数 $c, r$,表示小 R 的座位为第 $c$ 列第 $r$ 行。
【样例1输入】
2 2 99 100 97 98
【样例1输出】
1 2
【样例1说明】
按照成绩从高到低的顺序,成绩为 $100$ 的考生的座位为第 $1$ 列第 $1$ 行,成绩为 $99$ 的考生的座位为第 $1$ 列第 $2$ 行,成绩为 $98$ 的考生的座位为第 $2$ 列第 $2$ 行,成绩为 $97$ 的考生的座位为第 $2$ 列第 $1$ 行。小 R 的成绩为 $99$,因此座位为第 $1$ 列第 $2$ 行。
【样例2输入】
2 2 98 99 100 97
【样例2输出】
2 2
【样例2说明】
按照成绩从高到低的顺序,成绩为 $100$ 的考生的座位为第 $1$ 列第 $1$ 行,成绩为 $99$ 的考生的座位为第 $1$ 列第 $2$ 行,成绩为 $98$ 的考生的座位为第 $2$ 列第 $2$ 行,成绩为 $97$ 的考生的座位为第 $2$ 列第 $1$ 行。小 R 的成绩为 $98$,因此座位为第 $2$ 列第 $2$ 行。
【样例3输入】
3 3 94 95 96 97 98 99 100 93 92
【样例3输出】
3 1
【数据规模与约定】
对于所有测试数据,保证:
$1 \leq n \leq 10$, $1 \leq m \leq 10$;
对于所有 $1 \leq i \leq n \times m$,均有 $1 \leq a_i \leq 100$,且 $a_1, a_2, \dots, a_{n \times m}$ 互不相同。
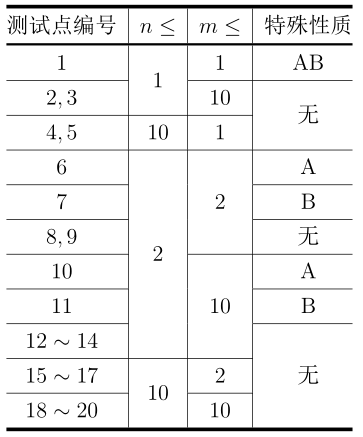
特殊性质 A:对于所有 $1 \leq i \leq n \times m$,均有 $a_i = i$。
特殊性质 B:对于所有 $1 \leq i \leq n \times m$,均有 $a_i = n \times m - i + 1$。