题目名称	3930. [CSP 2023J]旅游巴士
输入输出	`bus.in/out`
难度等级	★★☆
时间限制	1000 ms (1 s)
内存限制	512 MiB
测试数据	20
题目来源	syzhaoss 于2023-10-22加入
开放分组	全部用户
提交状态
分类标签	分层图
	分享题解

通过：17，提交：121，通过率：14.05%
LikableP	100	0.563 s	8.09 MiB	C++
syzhaoss	100	0.563 s	8.26 MiB	C++
金牌教师王艳芳	100	0.801 s	7.21 MiB	C++
金牌教师王艳芳	100	0.865 s	7.19 MiB	C++
cqw	100	1.116 s	11.23 MiB	C++
金牌教师王艳芳	100	1.370 s	5.53 MiB	C++
健康铀	100	1.567 s	7.42 MiB	C++
嗨嗨嗨	100	1.610 s	7.29 MiB	C++
whaleeee	100	1.665 s	8.29 MiB	C++
回归运动	100	1.739 s	70.33 MiB	C++

关于旅游巴士的近10条评论(全部评论)
- 通行后到达时间为 $T'' = T' + 1$，余数为 $(r + 1) \bmod k$； - 用 $T''$ 更新 $d[v][(r+1) \bmod k]$。最终答案为 $\min_{0 \leq r < k} d[n][r]$。金牌教师王艳芳 2025-10-12 15:39 8楼
有 $n$ 个景点、$m$ 条道路，巴士每 $k$ 分钟一班。每条道路有开放时间 $t_{\text{open}}$，仅当当前时间 $\geq t_{\text{open}}$ 时可通过，通行耗时 1 分钟。求从景点 $1$ 到景点 $n$ 的最早到达时间。思路：设 $d[i][r]$ 表示到达景点 $i$ 时，当前时间模 $k$ 余 $r$ 的最早绝对时间。初始状态 $d[1][0] = 0$。对每条边 $(u, v, t_{\text{open}})$，若当前时间为 $T = d[u][r]$，则： - 若 $T < t_{\text{open}}$，需等待至首个 $\geq t_{\text{open}}$ 的发车时刻：等待后时间 $T' = \left\lceil \frac{t_{\text{open}} - T}{k} \right\rceil \cdot k + T$；金牌教师王艳芳 2025-10-12 15:38 7楼
等待时间的计算：当我们需要在一条道路前等待时，计算公式为： \[ \text{等待周期数} = \left\lceil \frac{\text{开放时间} - \text{当前时间}}{k} \right\rceil \] 在代码中，我们使用整数除法来实现向上取整： \[ x = \frac{\text{na} - \text{nt} + k - 1}{k} \] 余数的计算：走过一条道路需要1分钟，所以新的余数为： \[ \text{新余数} = (\text{当前余数} + 1) \mod k \] AI转的一个latex版本的金牌教师王艳芳 2025-10-09 23:39 6楼
粘不完 `#include<bits/stdc++.h> using namespace std; int main(){ freopen("bus.in","r",stdin); freopen("bus.out","w",stdout); int n,m,k; cin>>n>>m>>k; int u[20005],v[20005],a[20005]; vector<int> g[10005]; for(int i=0;i<m;i++){ cin>>u[i]>>v[i]>>a[i]; g[u[i]].push_back(i); } int d[10005][105]; for(int i=1;i<=n;i++)for(int j=0;j<k;j++)d[i][j]=1000000000; d[1][0]=0; queue<pair<int,int>> q; q.push(make_pair(1,0)); while(!q.empty` 金牌教师王艳芳 2025-10-09 23:30 5楼
三年oi一场空，不开long long 见祖宗王和谐 2023-10-30 21:20 4楼
byd这题过不了了是吧在大街上倒立游泳 2023-10-26 20:47 3楼
卑鄙bus whaleeee 2023-10-24 20:43 2楼
#感谢教练#顶峰相见#沉淀三年#一场longlong毁了我的oi梦#中专开局又如何健康铀 2023-10-24 20:35 1楼

3930. [CSP 2023J]旅游巴士

★★☆ 输入文件：bus.in 输出文件：bus.out 简单对比
时间限制：1 s 内存限制：512 MiB

【题目描述】

小 Z 打算在国庆假期期间搭乘旅游巴士去一处他向往已久的景点旅游。

旅游景点的地图共有 $n$ 处地点，在这些地点之间连有 $m$ 条道路。其中 $1$ 号地点为景区入口，$n$ 号地点为景区出口。我们把一天当中景区开门营业的时间记为 $0$ 时刻，则从 $0$ 时刻起，每间隔 $k$ 单位时间便有一辆旅游巴士到达景区入口，同时有一辆旅游巴士从景区出口驶离景区。

所有道路均只能单向通行。对于每条道路，游客步行通过的用时均为恰好 $1$ 单位时间。

小 Z 希望乘坐旅游巴士到达景区入口，并沿着自己选择的任意路径走到景区出口，再乘坐旅游巴士离开，这意味着他到达和离开景区的时间都必须是 $k$ 的非负整数倍。由于节假日客流众多，小 Z 在旅游巴士离开景区前只想一直沿着景区道路移动，而不想在任何地点（包括景区入口和出口）或者道路上停留。

出发前，小 Z 忽然得知：景区采取了限制客流的方法，对于每条道路均设置了一个 “开放时间”$a _ i$，游客只有不早于 $a _ i$ 时刻才能通过这条道路。

请帮助小 Z 设计一个旅游方案，使得他乘坐旅游巴士离开景区的时间尽量地早。

【输入格式】

输入的第一行包含 3 个正整数 $n, m, k$，表示旅游景点的地点数、道路数，以及旅游巴士的发车间隔。

输入的接下来 $m$ 行，每行包含 3 个非负整数 $u _ i, v _ i, a_ i$，表示第 $i$ 条道路从地点 $u _ i$ 出发，到达地点 $v _ i$，道路的“开放时间”为 $a _ i$。

【输出格式】

输出一行，仅包含一个整数，表示小 Z 最早乘坐旅游巴士离开景区的时刻。如果不存在符合要求的旅游方案，输出 -1。

【样例输入1】

【样例输出1】

【样例 #1 解释】

小 Z 可以在 $3$ 时刻到达景区入口，沿 $1 \to 3 \to 4 \to 5$ 的顺序走到景区出口，并在 $6$ 时刻离开。

【样例 #2】

见附件中的 bus/bus2.in 与 bus/bus2.ans。

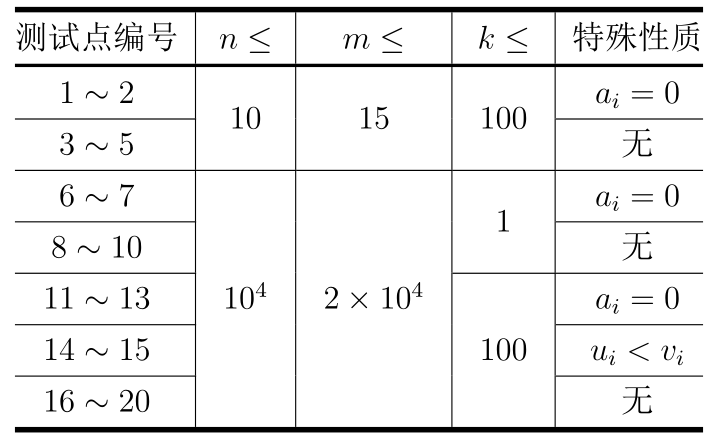
【数据范围】

对于所有测试数据有：$2 \leq n \leq 10 ^ 4$，$1 \leq m \leq 2 \times 10 ^ 4$，$1 \leq k \leq 100$，$1 \leq u _ i, v _ i \leq n$，$0 \leq a _ i \leq 10 ^ 6$。

关于旅游巴士的近10条评论(全部评论)
- 通行后到达时间为 $T'' = T' + 1$，余数为 $(r + 1) \bmod k$； - 用 $T''$ 更新 $d[v][(r+1) \bmod k]$。最终答案为 $\min_{0 \leq r < k} d[n][r]$。金牌教师王艳芳 2025-10-12 15:39 8楼
有 $n$ 个景点、$m$ 条道路，巴士每 $k$ 分钟一班。每条道路有开放时间 $t_{\text{open}}$，仅当当前时间 $\geq t_{\text{open}}$ 时可通过，通行耗时 1 分钟。求从景点 $1$ 到景点 $n$ 的最早到达时间。思路：设 $d[i][r]$ 表示到达景点 $i$ 时，当前时间模 $k$ 余 $r$ 的最早绝对时间。初始状态 $d[1][0] = 0$。对每条边 $(u, v, t_{\text{open}})$，若当前时间为 $T = d[u][r]$，则： - 若 $T < t_{\text{open}}$，需等待至首个 $\geq t_{\text{open}}$ 的发车时刻：等待后时间 $T' = \left\lceil \frac{t_{\text{open}} - T}{k} \right\rceil \cdot k + T$；金牌教师王艳芳 2025-10-12 15:38 7楼
等待时间的计算：当我们需要在一条道路前等待时，计算公式为： \[ \text{等待周期数} = \left\lceil \frac{\text{开放时间} - \text{当前时间}}{k} \right\rceil \] 在代码中，我们使用整数除法来实现向上取整： \[ x = \frac{\text{na} - \text{nt} + k - 1}{k} \] 余数的计算：走过一条道路需要1分钟，所以新的余数为： \[ \text{新余数} = (\text{当前余数} + 1) \mod k \] AI转的一个latex版本的金牌教师王艳芳 2025-10-09 23:39 6楼
粘不完 `#include<bits/stdc++.h> using namespace std; int main(){ freopen("bus.in","r",stdin); freopen("bus.out","w",stdout); int n,m,k; cin>>n>>m>>k; int u[20005],v[20005],a[20005]; vector<int> g[10005]; for(int i=0;i<m;i++){ cin>>u[i]>>v[i]>>a[i]; g[u[i]].push_back(i); } int d[10005][105]; for(int i=1;i<=n;i++)for(int j=0;j<k;j++)d[i][j]=1000000000; d[1][0]=0; queue<pair<int,int>> q; q.push(make_pair(1,0)); while(!q.empty` 金牌教师王艳芳 2025-10-09 23:30 5楼
三年oi一场空，不开long long 见祖宗王和谐 2023-10-30 21:20 4楼
byd这题过不了了是吧在大街上倒立游泳 2023-10-26 20:47 3楼
卑鄙bus whaleeee 2023-10-24 20:43 2楼
#感谢教练#顶峰相见#沉淀三年#一场longlong毁了我的oi梦#中专开局又如何健康铀 2023-10-24 20:35 1楼