| 题目名称 | 4118. [统一省选 2025]推箱子 |
|---|---|
| 输入输出 | move.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:2, 提交:8, 通过率:25% | ||||
|
|
100 | 11.509 s | 15.96 MiB | C++ |
|
|
100 | 12.349 s | 33.99 MiB | C++ |
|
|
52 | 14.594 s | 15.95 MiB | C++ |
|
|
52 | 14.629 s | 15.95 MiB | C++ |
|
|
52 | 14.736 s | 15.98 MiB | C++ |
|
|
16 | 12.606 s | 15.95 MiB | C++ |
|
|
0 | 5.359 s | 3.05 MiB | C++ |
|
|
0 | 5.389 s | 3.03 MiB | C++ |
| 关于 推箱子 的近10条评论(全部评论) |
|---|
【题目描述】
在一条无穷长的数轴上摆放着 $n$ 个箱子。第 $i$ ($1 \leq i \leq n$) 个箱子在时刻 0 位于数轴 $a_i$ 处,而你希望在时刻 $t_i$ 以及之后的所有时刻,这个箱子处在数轴的 $b_i$ 处。保证序列 $[a_1, \ldots, a_n]$ 和 $[b_1, \ldots, b_n]$ 单调递增。
为此,从时刻 $0$ 开始的每个单位时间里,你可以将某个箱子在数轴上移动一个单位长度,也可以什么都不做。你需要保证任意时刻每个点上都只有一个箱子。形式化地,每个单位时间里你可以按照以下方式进行一次操作,也可以不进行操作:
1. 选择任意一个箱子。记其编号为 $i$,它目前的位置为 $p_i$。
2. 选择一个方向 $d \in \{\pm1\}$,其中 $d = 1$ 代表向右,$d = -1$ 代表向左。你需要保证数轴上 $(p_i + d)$ 处没有箱子。
3. 将 $i$ 号箱子从点 $p_i$ 移动到点 $(p_i + d)$ 处。
你想知道,是否存在一种操作方法同时满足所有箱子的要求,即对于任意 $1 \leq i \leq n$,第 $i$ 个箱子在时刻 $t_i$ 以及之后的所有时刻都处于数轴的 $b_i$ 处。
【输入格式】
本题有多组测试数据。输入的第一行两个整数 $c, T$,分别表示测试点编号和测试数据组数,接下来输入每组测试数据。样例满足 $c = 0$。
对于每组测试数据,第一行一个整数 $n$,表示箱子的个数,接下来 $n$ 行,第 $i$ ($1 \leq i \leq n$) 行三个整数 $a_i, b_i, t_i$,分别表示第 $i$ 个箱子的初始位置、目标位置和时刻要求。
【输出格式】
对于每组测试数据,输出一行一个字符串 `Yes` 或 `No`,表示是否存在一种操作方法同时满足所有箱子的要求。
【样例输入】
0 2 2 4 5 1 6 7 1 3 4 5 3 7 6 1 10 8 4
【样例输出】
No Yes
【样例说明】
该组样例共有 2 组测试数据。
- 对于第一组测试数据,答案是否定的。将 1 号箱子由点 4 移动到点 5,并将 2 号箱子由点 6 移动到点 7,至少需要两个单位时间,因此不可能在时刻 1 同时满足两个箱子的条件。
- 对于第二组测试数据,答案是肯定的,例如如下方法同时满足了所有箱子的要求:
- 在时刻 0 至时刻 1 的一个单位时间,将 2 号箱子由点 7 移动到点 6;
- 在时刻 1 至时刻 2 的一个单位时间,将 3 号箱子由点 10 移动到点 9;
- 在时刻 2 至时刻 3 的一个单位时间,将 1 号箱子由点 4 移动到点 5;
- 在时刻 3 至时刻 4 的一个单位时间,将 3 号箱子由点 9 移动到点 8;
- 在之后的所有单位时间,什么都不做。
【数据规模与约定】
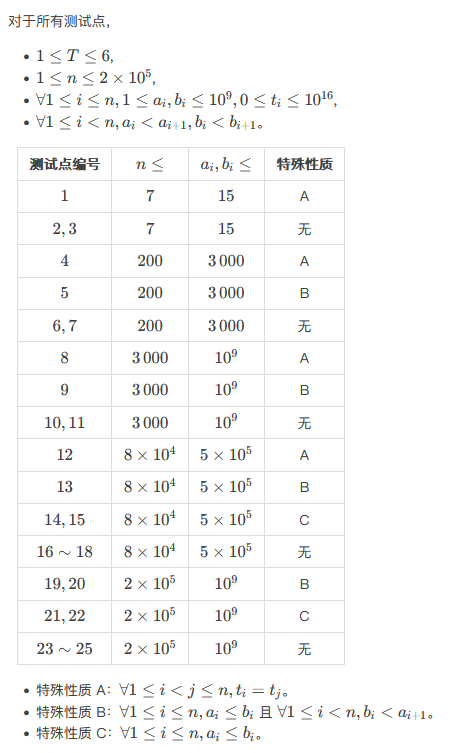
【来源】
2025联合省选day2T1