| 题目名称 | 3896. [桐柏一中邀请赛S13]琉金云间 |
|---|---|
| 输入输出 | bracket.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:0, 通过率:0% | |||
| 关于 琉金云间 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
看得出来作者很喜欢宵宫
2024-07-10 10:11
1楼
| ||||
【题目背景】
Yoimiya 和云浅在梦里看烟花。烟花在梦中排列成了括号的形状。
【题目描述】
合法括号串的定义如下:
• 空串是合法括号串。
• 如果 A 是合法括号串,那么 (A) 也是合法括号串。
• 如果 A和B 都是合法括号串,那么 AB 也是合法括号串。其中 AB 表示把字符串 A 和字符串 B 拼接在一起形成的字符串。
Yoimiya 定义一个长为 $2n$ 的合法括号串 $S$ 对应的括号树 $T$ 是一棵有根树,它的构造方式如下:
• 按照 $i=1,2,\cdots, 2n$的顺序遍历括号串 $S$,并维护当前节点 $u$。
• 一开始,树中只有一个节点 $u$,其编号为 $1$。
• 若 $S_i = $(,则新建节点 $u$ 的儿子节点 $v$,$v$ 的编号是当前节点的总数 $+1$;然后把当前节点 $u$ 改为 $v$。
• 若 $S_i =$ ),则将当前节点 $u$ 改为他的父亲节点。可以证明此时 $u$ 一定存在父亲节点。
例如,对于合法括号串 (()())(),Yoimiya 构造出的括号树如图所示:
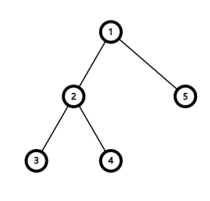
不难发现,对于一个长度为 $2n$ 的合法括号串,其对应的括号树是一棵 $n + 1$ 个节点的有根树,其中根节点为 $1$ 号节点。
定义一个合法括号串的得分为其对应的括号树上所有结点的深度之和,其中树上一个结点的深度是它到根节点所需要经过的最小点数。例如,对于上面的括号序列 (()())(),其得分就是 $1+2+3+3+2 = 11$。
现在给出一个长度为 $2n$ 的合法括号串,其中有一些位置的字符已经确定,另外一些位置的字符尚未确定(用 ? 表示)。Yoimiya 想要算出,对于所有可能的将未确定的位置一一确定的方案,所得到的所有合法括号串的得分之和对 $998244353$ 取模的值是多少。
【输入格式】
第一行一个正整数 $n$ 表示括号序列的长度。
第二行一个长度为 $2n$ 的字符串 $S$ 表示尚未完全确定的合法括号串。
【输出格式】
输出一行一个整数表示答案。
【样例1输入】
4 (?)??)?)
【样例1输出】
34
【样例1说明】
一共有以下 3 种可能的合法括号串:
• (()(())),其得分为 $1 + 2 + 3 + 3 + 4 = 13$。
• (()())(),其得分为 $1 + 2 + 3 + 3 + 2 = 11$。
• (())()(),其得分为 $1 + 2 + 3 + 2 + 2 = 10$。
故所有方案的得分之和为 $13 + 11 + 10 = 34$。
【样例2/3/4下载】
【数据规模与约定】
下文中记 $m = 2n$。对于所有测试点,有 $1 ≤ m ≤ 500$。每个测试点的具体限制见下表:
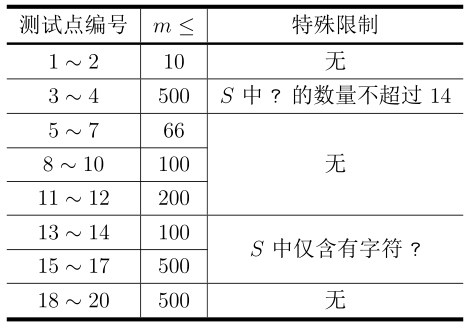
【来源】
桐柏一中邀请赛S13 Task4