| 题目名称 | 3879. [省选 2023]城市建造 |
|---|---|
| 输入输出 | cities.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:0, 通过率:0% | |||
| 本题关联比赛 | |||
| 2025.2.24 | |||
| 省选2023Day1复现 | |||
| 关于 城市建造 的近10条评论(全部评论) |
|---|
【题目描述】
在这个国度里面有 $n$ 座城市,一开始城市之间修有若干条双向道路,导致这些城市形成了 $t \ge 2$ 个连通块,特别的,这些连通块之间两两大小差的绝对值不超过 $0 \le k \le 1$。为了方便城市建设与发展,$n$ 座城市中的某 $t$ 座城市在这 $t$ 座城市之间额外修建了至少一条双向道路,使得所有城市连通。
现在已经知道额外修建后的所有道路,你需要算出有哪些双向道路集合 $E'$,满足这些道路有可能是后来额外修建的,请输出答案对 $998,244,353$ 取模的结果。
即给定一张 $n$ 个点 $m$ 条边的无向连通图 $G = (V, E)$,询问有多少该图的子图 $G' = (V', E')$,满足 $E' \ne \emptyset$ 且 $G - E'$ 中恰好有 $|V'|$ 个连通块,且任意两个连通块大小之差不超过 $k$,保证 $0 \le k \le 1$,请输出答案对 $998,244,353$ 取模的结果。
【输入格式】
输入的第一行包含三个正整数 $n, m, k$,分别表示城市数、修建后的道路数以及任意两个连通块大小之差的上限。
接下来 $m$ 行每行包含两个正整数 $u, v$,表示城市 $u$ 和 $v$ 之间存在一条双向道路,保证 $u \ne v$。
【输出格式】
输出一个数表示答案对 $998,244,353$ 取模后的结果。
【样例1输入】
4 4 1 1 2 2 3 1 3 3 4
【样例1输出】
2
【样例1说明】
有以下两种情况:
·本来只有 $(3, 4)$ 这一条道路,此时有三个连通块,分别为 $\{1\}, \{2\}, \{3, 4\}$;后来城市 $1, 2, 3$ 决定在它们三座城市中额外修建了 $(1, 2), (2, 3), (1, 3)$ 这三条道路,使得所有城市连通。
·本来没有任何道路,此时有四个连通块,分别为 $\{1\}, \{2\}, \{3\}, \{4\}$;后来城市 $1, 2, 3, 4$ 决定在它们四座城市中额外修建了 $(1, 2), (2, 3), (1, 3), (3, 4)$ 这四条道路,使得所有城市连通。
【样例下载】
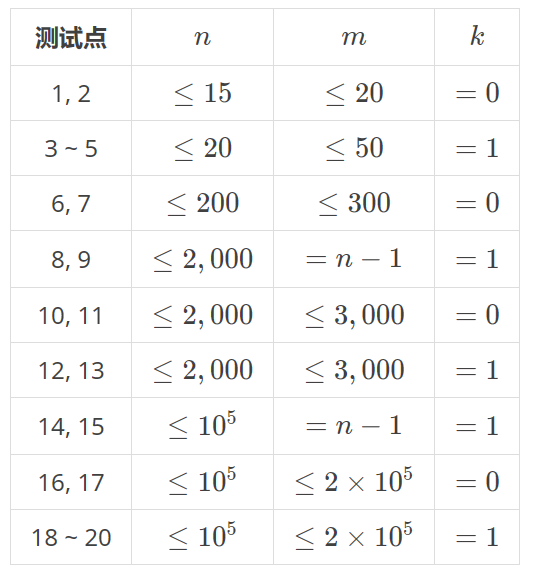
【数据规模与约定】
对于所有的数据,保证:$3 \le n \le 10^5$,$n - 1 \le m \le 2 \times 10^5$,$0 \le k \le 1$。
【来源】
统一省选 2023 Day1 Task2