| 题目名称 | 1484. [UVa 1069] 总是整数 |
|---|---|
| 输入输出 | Integer.in/out |
| 难度等级 | ★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:2, 提交:3, 通过率:66.67% | ||||
|
|
100 | 0.009 s | 0.31 MiB | C++ |
|
|
100 | 0.019 s | 0.31 MiB | C++ |
|
|
70 | 0.032 s | 0.22 MiB | C++ |
| 关于 总是整数 的近10条评论(全部评论) |
|---|
【题目描述】
组合数学主要研究计数问题。比如,
-从 $n$ 个人中选 $2$ 个人的方法有多少种方法?
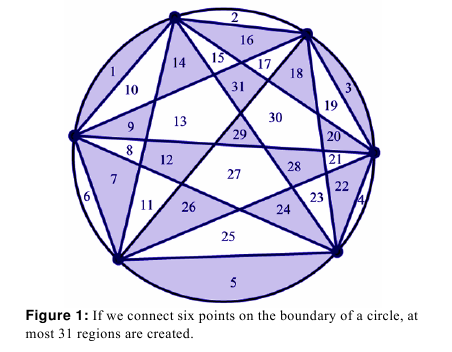
-圆周上有 $n$ 个点,两两相连之后最后能把圆面分成多少部分?
-有一个金字塔,从塔顶开始每一层分别有,$1×1,2×2,...n×n$ 个小正方体,问一共有多少个小立体?
很多问题的答案都可以被写成多项式的形式。对应上面的问题,答案是:
- n(n-1)/2
- (n^4 - 6n^3 + 23n^2 - 18^n + 24)/24
- n(n + 1)(2n + 1)/6, or (2n^3 + 3n^2 + n)/6
由于上述 $3$ 个多项式都是计数问题的答案,因此当 $n$ 取任意正整数时,这些多项式的值都是整数。当然,对于其他多项式,这个性质并不一定成立。
给一个形式如 P/D (其中 $P$ 是整系数多项式,$D$ 是正整数)的多项式,判断它是否在所有正整数处取的整数值。
【输入格式】
输入包含多组数据。每组数据仅一行,即一个多项式 (P)/D,其中P是若干个形如 Cn^E 的项之和,其中系数 $C$ 和 $E$ 满足以下条件:
(1)$E$ 是一个满足 $0≤E≤100$ 的整数。如果 $E=0$,则 Cn^E 写成 $C$;如果 $E=1$,Cn^E 写成 Cn,除非 $C=1$ 或者 $-1$($c=1$ 时写成 $n=-1$ 是写成 $-n$).
(2)$C$ 是一个整数。如果 $C$ 为 $1$ 或 $-1$ 且 $E$ 不是 $0$ 或 $1$,则 Cn^E 写成 n^E 或 -n^E.
(3)只有不在第一项的非负 $C$ 的前面才会有一个加号。
(4)$E$ 的数值严格递减。
(5)$C$ 和 $D$ 都在 $32$ 位带符号整数范围内。
输入结束标志为单个句号(.)。
【输出格式】
对于每组数据,如果满足条件,输入"Always an integer",否则输出"Not always an integer"
【样例输入】
(n^2-n)/2 (2n^3+3n^2+n)/6 (-n^14-11n+1)/3 .
【样例输出】
Case 1: Always an integer Case 2: Always an integer Case 3: Not always an integer
【提示】
Difference Series
【来源】
UVa 1069 Always an Integer,World Finals 2008,LA 4119
刘汝佳,《算法竞赛入门经典训练指南》表2.4