| 题目名称 | 3467. [NOI 2020]时代的眼泪 |
|---|---|
| 输入输出 | tears.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 4000 ms (4 s) |
| 内存限制 | 1024 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:0, 通过率:0% | |||
| 关于 时代的眼泪 的近10条评论(全部评论) |
|---|
【题目描述】
小 L 喜欢与智者交流讨论,而智者也经常为小 L 出些思考题。
这天智者又为小 L 构思了一个问题。智者首先将时空抽象为了一个二维平面,进而将一个事件抽象为该平面上的一个点,将一个时代抽象为该平面上的一个矩形。
为了方便,下面记 (a,b)≤(c,d) 表示平面上两个点 (a,b),(c,d) 满足 a≤c,b≤d。
更具体地,智者给定了 n 个事件,他们用平面上 n 个不同的点 $\{(x_i,y_i)\}_{i=1}^n$ 来表示;智者还给定了 m 个时代,每个时代用平面上一个矩形$r_{i,1},r_{i,2},c_{i,1},c_{i,2}$ 来表示,其中 $(r_{i,1},c_{i,1})$是矩形的左下角,$(r_{i,2},c_{i,2})$是矩形的右上角,保证 $(r_{i,1},c_{i,1})$≤$(r_{i,2},c_{i,2})$。我们称时代 i 包含了事件 j 当且仅当 $(r_{i,1},c_{i,1})$≤(xj,yj)≤$(r_{i,2},c_{i,2})$。
智者认为若两个事件 i,j 满足 (xi,yi)≤(xj,yj),则这两个事件形成了一次遗憾。而对一个时代内包含的所有事件,它们所形成的遗憾被称为这个时代的眼泪,而形成的遗憾次数则称为该时代的眼泪的大小。现在智者想要小 L 计算每个时代的眼泪的大小。
小 L明白,如果他回答不了这个问题,他也将成为时代的眼泪,请你帮帮他。
【输入格式】
第一行两个整数 n,m,分别表示事件数与时代数。
第二行 n 个整数 pi,其中第 i 个数表示事件 i 在平面上的坐标为 (i,pi)。保证 pi 为一个 1 到 n 的排列。
之后 m 行,每行四个整数$r_{i,1},r_{i,2},c_{i,1},c_{i,2}$,表示每个时代对应的矩形。
【输出格式】
输出 m 行,每行包含一个整数,第 i 行输出第 i 个时代的眼泪的大小。
【样例输入】
9 9 9 8 7 6 2 4 5 3 1 4 9 3 6 2 9 1 8 3 8 2 4 3 9 2 7 2 8 1 6 1 9 1 9 1 3 5 7 2 3 3 3 6 6 6 6
【样例输出】
1 4 2 4 4 4 0 0 0
【样例解释】
对于时代 1,包含的遗憾有 (6,7)(即事件 6 与事件 7 形成的遗憾,下同)。
对于时代 2,包含的遗憾有 (5,6),(6,7),(5,7),(5,8)。
对于时代 3,包含的遗憾有 (5,6),(5,8)。
对于时代 4,包含的遗憾有 (5,6),(6,7),(5,7),(5,8)。
对于时代 5,包含的遗憾有 (5,6),(6,7),(5,7),(5,8)。
对于时代 6,包含的遗憾有 (5,6),(6,7),(5,7),(5,8)。
对于时代 7,8,9,它们均不包含任何遗憾。
【数据范围】
对于所有测试点:1≤n≤10^5,1≤m≤2×10^5,1≤$r_{i,1},r_{i,2},c_{i,1},c_{i,2}$≤n。
每个测试点的具体限制见下表:
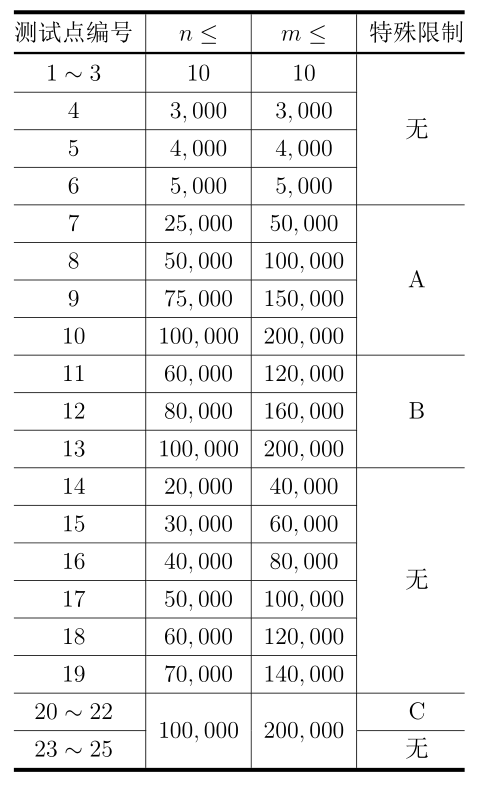
特殊限制 A:对于所有时代 i 有 $c_{i,1}=1,c_{i,2}=n$。
特殊限制 B:任意两个不同时代所代表的矩形,它们要么是包含关系(一个矩形在另一个矩形内,边界允许重合),要么是相离关系(两矩形不包含共同点,边界不允许重合)。
特殊限制 C:最多有 50 对事件 (i,j)(1≤i<j≤n) 不满足 (i,pi)≤(j,pj)。
【来源】
NOI2020 Day1 Task3