| 题目名称 | 4230. [NOIP 2025 T2]清仓甩卖 |
|---|---|
| 输入输出 | sale.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:6, 提交:8, 通过率:75% | ||||
|
|
100 | 1.842 s | 3.73 MiB | C++ |
|
|
100 | 2.490 s | 4.07 MiB | C++ |
|
|
100 | 3.019 s | 117.92 MiB | C++ |
|
|
100 | 3.293 s | 3.84 MiB | C++ |
|
|
100 | 4.064 s | 117.80 MiB | C++ |
|
|
100 | 6.103 s | 231.54 MiB | C++ |
|
|
92 | 6.588 s | 117.88 MiB | C++ |
|
|
0 | 0.106 s | 4.03 MiB | C++ |
| 关于 清仓甩卖 的近10条评论(全部评论) |
|---|
【题目描述】
小 X 的糖果促销策略很成功,现在糖果店只剩下了 $n$ 颗糖果,其中第 $i$ ($1 \le i \le n$) 颗糖果的原价为 $a_i$ 元。小 X 计划将它们全部重新定价,清仓甩卖。具体地,小 X 会将每颗糖果的清仓价格分别定为 1 元或 2 元。设第 $i$ ($1 \le i \le n$) 颗糖果的清仓价格为 $w_i \in \{1,2\}$ 元,则它的性价比被定义为原价与清仓价格的比值,即 $\frac{a_i}{w_i}$。
小 R 又带了 $m$ 元钱买糖果。这一次,小 R 希望他购买到的糖果的原价总和最大,于是他采用了以下购买策略:将所有糖果按照性价比从大到小排序,然后依次考虑每一颗糖果。具体地,若小 R 在考虑第 $i$ ($1 \le i \le n$) 颗糖果时剩余的钱至少为 $w_i$ 元,则他会购买这颗糖果;否则他会跳过这颗糖果,继续考虑下一颗。特别地,若存在两颗糖果的性价比相同,则小 R 会先考虑原价较高的糖果;若存在两颗糖果的性价比与原价均相同,则小 R 会先考虑编号较小的糖果。
例如,若小 X 的糖果商店剩余 3 颗糖果,原价分别为 $a_1=1$,$a_2=3$,$a_3=5$,而清仓价格分别为 $w_1=w_2=1$,$w_3=2$,则性价比分别为 $1, 3, \frac{5}{2}$。因此小 R 会先考虑第 2 颗糖果,然后考虑第 3 颗糖果,最后考虑第 1 颗糖果。
小 R 想知道,在小 X 的所有 $2^n$ 种定价方案中,有多少种定价方案使得他按照上述购买策略能购买到的糖果的原价总和最大。你需要帮助小 R 求出满足要求的定价方案的数量。由于答案可能较大,你只需要求出答案对 $998,244,353$ 取模后的结果。
【输入格式】
本题包含多组测试数据。
输入的第一行包含两个非负整数 $c, t$,分别表示测试点编号与测试数据组数。$c=0$ 表示该测试点为样例。
接下来依次输入每组测试数据,对于每组测试数据:
第一行包含两个正整数 $n, m$,分别表示糖果的数量与小 R 的钱数;
第二行包含 $n$ 个正整数 $a_1, a_2, \ldots, a_n$,分别表示每颗糖果的原价。
【输出格式】
对于每组测试数据,输出一行一个非负整数,表示使得小 R 购买到的糖果的原价总和达到最大值的定价方案数对 $998,244,353$ 取模后的结果。
【样例 1 输入】
0 1 3 2 1 3 5
【样例 1 输出】
6
【样例 1 说明】
该样例即为题目描述中的例子。共有以下 6 种定价方案使得小 R 购买到的糖果原价总和最大,分别为:
$w_1 = w_2 = w_3 = 1$,小 R 购买到的糖果原价总和为 8;
$w_1 = w_3 = 1$,$w_2 = 2$,小 R 购买到的糖果原价总和为 6;
$w_1 = 1$,$w_2 = w_3 = 2$,小 R 购买到的糖果原价总和为 5;
$w_2 = w_3 = 1$,$w_1 = 2$,小 R 购买到的糖果原价总和为 8;
$w_3 = 1$,$w_1 = w_2 = 2$,小 R 购买到的糖果原价总和为 5;
$w_1 = w_2 = w_3 = 2$,小 R 购买到的糖果原价总和为 5。
注意:若 $w_1 = w_2 = 1$,$w_3 = 2$,则小 R 会依次购买第 2 颗和第 1 颗糖果,原价总和为 4,但小 R 可以只购买第 3 颗糖果,原价总和为 5。因此该定价方案无法使小 R 购买到的糖果的原价总和达到最大值。
【样例 2】
见选手目录下的 sale/sale2.in 与 sale/sale2.ans。
该样例满足测试点 $1 \sim 3$ 的约束条件。
【样例 3】
见选手目录下的 sale/sale3.in 与 sale/sale3.ans。
该样例满足测试点 $4,5$ 的约束条件。
【样例 4】
见选手目录下的 sale/sale4.in 与 sale/sale4.ans。
该样例满足测试点 $7 \sim 9$ 的约束条件。
【样例 5】
见选手目录下的 sale/sale5.in 与 sale/sale5.ans。
该样例满足测试点 $10 \sim 12$ 的约束条件。
【样例 6】
见选手目录下的 sale/sale6.in 与 sale/sale6.ans。
该样例满足测试点 $13$ 的约束条件。
【样例 7】
见选手目录下的 sale/sale7.in 与 sale/sale7.ans。
该样例满足测试点 $14,15$ 的约束条件。
【样例 8】
见选手目录下的 sale/sale8.in 与 sale/sale8.ans。
该样例满足测试点 $17$ 的约束条件。
【样例 9】
见选手目录下的 sale/sale9.in 与 sale/sale9.ans。
该样例满足测试点 $19,20$ 的约束条件。
【样例 10】
见选手目录下的 sale/sale10.in 与 sale/sale10.ans。
该样例满足测试点 $21 \sim 23$ 的约束条件。
【样例 11】
见选手目录下的 sale/sale11.in 与 sale/sale11.ans。
该样例满足测试点 $24,25$ 的约束条件。
【数据范围】
设 $N$ 为单个测试点内所有测试数据的 $n$ 的和。对于所有测试数据,均有:
$1 \le t \le 5 \times 10^4$;
$1 \le n \le 5,000$,$N \le 5 \times 10^4$,$1 \le m \le 2n-1$;
对于所有 $1 \le i \le n$,均有 $1 \le a_i \le 10^9$。
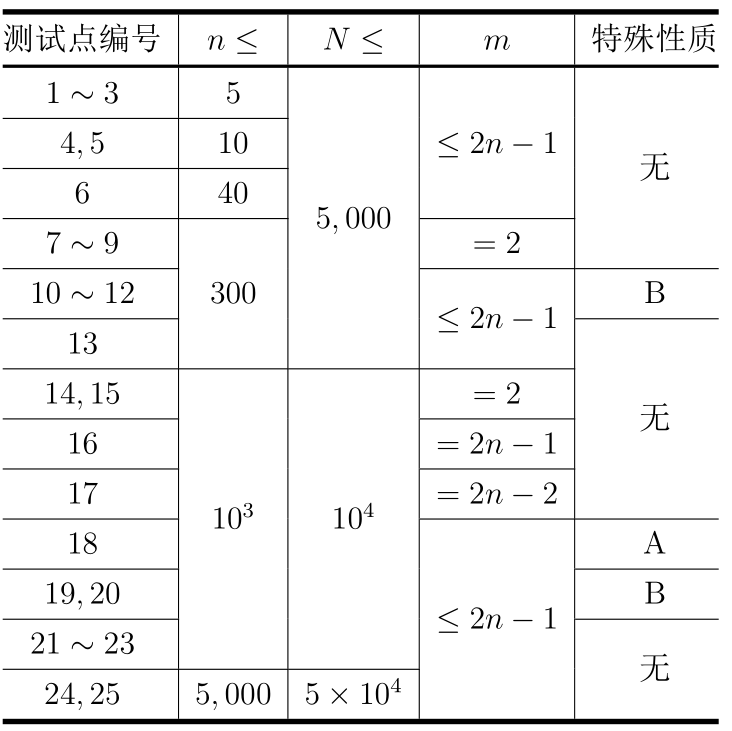
特殊性质 A:$a_1 = a_2 = \cdots = a_n$。
特殊性质 B:对于所有 $1 \le i \le n$,均有 $a_i > 5 \times 10^8$。