| 题目名称 | 2435. [HZOI 2016]艾米利亚的魔法融合 |
|---|---|
| 输入输出 | aimiliyademagicmix.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:33, 提交:55, 通过率:60% | ||||
|
|
100 | 0.841 s | 51.79 MiB | C |
|
|
100 | 1.361 s | 200.59 MiB | C++ |
|
|
100 | 1.413 s | 51.79 MiB | C |
|
|
100 | 1.435 s | 51.79 MiB | C |
|
|
100 | 2.204 s | 150.97 MiB | C++ |
|
|
100 | 2.257 s | 124.27 MiB | C++ |
|
|
100 | 2.279 s | 200.56 MiB | C++ |
|
|
100 | 2.347 s | 243.50 MiB | C++ |
|
|
100 | 2.356 s | 146.19 MiB | C++ |
|
|
100 | 2.506 s | 162.44 MiB | C++ |
| 关于 艾米利亚的魔法融合 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
2018-09-01 12:51
9楼
| ||||
|
艾米利亚的党赛高
| ||||
|
mu(p) * mu(p) == 4 , 再一次身败名裂
2016-12-25 07:44
7楼
| ||||
|
受functional programming影响颇深啊
| ||||
|
发现O(n+n)的和O(n+sqrt(n))的几乎一样快
2016-12-11 19:05
5楼
| ||||
|
卧槽
线性筛都会T 让不让人活了 好吧稍微优化一下还是可以过的
2016-10-05 14:48
4楼
| ||||
|
hhhh
出题人666
2016-08-18 18:49
3楼
| ||||
|
光粒打击... 我的二向箔哪?
2016-08-13 21:23
2楼
| ||||
|
%%%
2016-08-13 21:19
1楼
| ||||
2435. [HZOI 2016]艾米利亚的魔法融合
★★★ 输入文件:aimiliyademagicmix.in
输出文件:aimiliyademagicmix.out
简单对比时间限制:3 s 内存限制:512 MiB
【题目描述】
艾米利亚的魔法融合
aimiliyademagicmix
上一次,菜月昴找出了艾米利亚的暗金色冰元素的规律,通过运用四维空间泡上的无形波动成功衰竭了艾米利亚的魔法。但是这个魔法散发出来的余威还是震慑到了帕克。
“你们的魔法强度实在很大,几乎都已经接近了光粒打击的强度了”帕克如是说到。
“我认为,你们应该妥善地处理一下这融合魔法的力量,这将对你的王选有很大的推进作用”贝蒂突然出现在了众人的眼前。
“贝蒂!你不是去参加八维空间的开拓战争了吗?”艾米利亚问道。
“啊。。。那个啊。。。他们说我这样的没有强力攻击的精灵根本无法对战争产生实质性的效果,所以直接把我传送回来了。”贝蒂丝毫不掩饰。
“王选已经迫在眉睫了,艾米利亚,你的咒语强度不错,几乎等同于光粒打击了,只要你们能好好地运用这股力量,肯定没有人能挡住你们”
“可是现在的问题就是,你们的力量要怎么融合才能达到最大的效果”帕克担心的问道
“这个简单,只要每一次融合的时候,都携带着这个信息就可以了”贝蒂翻了翻书。
“只要菜月昴你在你的元素中携带刻印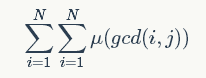 的值,就可以成功地融合魔力了”贝蒂非常肯定地说道。
的值,就可以成功地融合魔力了”贝蒂非常肯定地说道。
但是,就在这时,正在看题的你突然感觉到一股诡异的波动。
我去!菜月昴那小子通过四维空间泡上的无形波动,穿过了无数的低光速黑洞通过wifi连接到了你。。。
(⊙o⊙)…,,,这次菜月昴那小子传过来的图倒不错。。。

【输入格式】
一行,为一个正整数N;(μ表示莫比乌斯函数)
【输出格式】
一行,为一个正整数,表示计算式的值
【样例输入1】
10
【样例输出1】
35
【样例输入2】
100
【样例输出2】
3631
【提示】
对于30%的数据,N<=10^4
对于100%的数据,N<=10^7
对于μ函数的求法是这样的:
μ(1)默认为1,对于一个数,将之分解(10=2*5),
假如分解的每一个质数的指数都是1,且分解出r个质数,那么此数的值为(-1)^r。
如果指数并不全都是1,那么此数就是0。
【来源】
HZOI 2016