| 题目名称 | 4250. 时空跳跃 |
|---|---|
| 输入输出 | timejump.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 查看题解 | 分享题解 |
| 通过:2, 提交:4, 通过率:50% | ||||
|
|
100 | 0.711 s | 19.63 MiB | C++ |
|
|
100 | 0.720 s | 19.55 MiB | C++ |
|
|
60 | 4.472 s | 13.22 MiB | C++ |
|
|
20 | 8.814 s | 3.70 MiB | C++ |
| 本题关联比赛 | |||
| 期末考试0 | |||
| 关于 时空跳跃 的近10条评论(全部评论) |
|---|
【题目背景】
Madoka 又一次永远离开了 Homura,为了拯救 Madoka,Homura 决定再一次时间跳跃来挽回一切。
【题目描述】
因为 Homura 在无尽的轮回中,灵魂宝石逐渐变得浑浊,所以她只能使用有限制的时间回溯魔法。
具体的,不同的时间节点被被一些特殊事件连接,形成了一个树形的结构,Homura 的时间魔法就是在这颗树上进行。这是一个 $n$ 个节点以 $1$ 为根的有根树,对于第 $2\leq i\leq n$ 个节点,其父亲 $f_i$ 在 $[l_i,r_i]$ 中均匀随机。每个边有边权,初始为 $0$。
每次,Homura 可以移动到当前时间节点相邻的时间节点,她要进行 $m$ 次时间跳跃,每次跳跃将沿着最短路径从 $u_i$ 移动到 $v_i$,Homura 每经过一条边,就会留下标记,使经过的边权值加上 $w_i$。
长期的轮回让 Homura 身心俱疲,她已经忘了自己的标记,她希望你对于所有 $i=2\sim n$,求 $(i,f_i)$ 边上权值的期望,对 $998244353$ 取模。
如何在模意义下作除法:若 $p,M$ 互质且存在 $\frac{a}{p}\equiv aq\pmod{M}$,则 $q=p^{M-2}$,换言之,在 $M$ 意义下,你可以用 $a$ 乘上 $q$ 代替 $a$ 除以 $p$。
【输入格式】
第一行一个正整数表示 $n$。
接下来 $n-1$ 行,其中第 $i$ 行两个正整数表示 $l_{i+1},r_{i+1}$。
接下来一行一个正整数表示 $m$。
接下来 $m$ 行,第 $i$ 行三个正整数表示 $u_i,v_i,w_i$。
【输出格式】
一行 $n-1$ 个正整数,其中第 $i$ 个表示边 $(i+1,f_{i+1})$ 边权的期望,对 $998244353$ 取模。
【样例输入1】
3 1 1 1 2 1 1 3 2
【样例输出1】
1 2
【样例输入2】
5 1 1 1 2 3 3 2 4 9 2 5 497855355 1 5 840823564 3 1 295265328 2 3 457999227 4 4 235621825 2 1 86836399 5 2 800390742 5 3 869167938 2 4 269250165
【样例输出2】
405260353 409046983 606499796 13504540
【样例说明】
对于第一个样例,所有节点的父亲共有 $2$ 种可能的情况:
$f_2=1,f_3=1$,此时 $(f_2,2),(f_3,3)$ 边上的权值分别是 $0,2$。
$f_2=1,f_3=2$,此时 $(f_2,2),(f_3,3)$ 边上的权值分别是 $2,2$。
于是边 $(f_2,2)$ 边权的期望为 $\frac{0+2}{2}=1$,边 $(f_3,3)$ 边权的期望为 $\frac{2+2}{2}=2$。
【数据规模与约定】
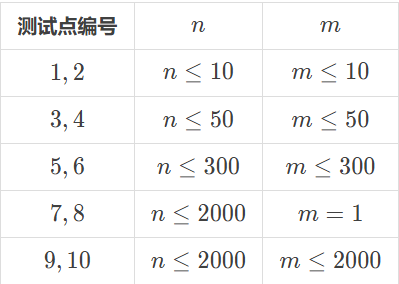
对于所有数据,满足 $1\le u_i,v_i\le n,1\le w_i\le 10^9,1\le l_i\le r_i<i$。
大样例,所有大样例均无特殊性质。
【来源】
luogu P10879。