| 题目名称 | 3104. [HAOI 2019]字符串问题 |
|---|---|
| 输入输出 | string.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 6000 ms (6 s) |
| 内存限制 | 1024 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:9, 通过率:11.11% | ||||
|
|
100 | 31.592 s | 100.85 MiB | C++ |
|
|
80 | 14.187 s | 351.25 MiB | C++ |
|
|
80 | 39.954 s | 231.03 MiB | C++ |
|
|
50 | 32.379 s | 136.40 MiB | C++ |
|
|
30 | 42.340 s | 15.55 MiB | C++ |
|
|
10 | 43.904 s | 22.99 MiB | C++ |
|
|
0 | 0.000 s | 0.00 MiB | C++ |
|
|
0 | 0.112 s | 3.16 MiB | C++ |
|
|
0 | 3.112 s | 50.94 MiB | C++ |
| 本题关联比赛 | |||
| HAOI2019 Day1 | |||
| 关于 字符串问题 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
抢楼!省选留念
2019-04-09 20:29
1楼
| ||||
【题目背景】
Yazid 和 Tiffany 喜欢字符串问题。在这里,我们将给你介绍一些关于字符串的基本概念。
对于一个字符串 $S$ ,我们定义 $|S|$ 表示 $S$ 的长度。
接着,我们定义该串的子串 $S(L,R)$ 表示由 $S$ 中从左往右数,第 $L$ 个字符到第 $R$ 个字符依次连接形成的字符串,特别地,如果 $L<1$ 或 $R>|S|$或 $L>R$,则 $S(L,R)$ 表示空串。
我们说两个字符串相等,当且仅当它们的长度相等,且从左至右各位上的字符依次相同。
我们说一个字符串 $T$ 是 $S$ 的前缀,当且仅当 $S(1,|T|) = T$。
两个字符串 $S,T$ 相加 $S+T$ 表示的是在 $S$ 后紧挨着写下 $T$ 得到的长度为 $|S| + |T|$ 的字符串。
【题目描述】
现有一个字符串 $S$。
Tiffany 将从中划出 $n_a$ 个子串作为 $A$ 类串,第 $i$ 个($1\leq i\leq n_a$)为$A_i=S(la_i,ra_i)$。
类似地,Yazid 将划出 $n_b$ 个子串作为 $B$ 类串,第 $i$ 个($1\leq i\leq n_b$)为 $B_i=S(lb_i,rb_i)$。
现额外给定 $m$ 组支配关系,每组支配关系 $(x,y)$ 描述了第 $x$ 个 $A$ 类串支配 第 $y$ 个 $B$ 类串。
求一个长度最大的目标串 $T$,使得存在一个串 $T$ 的分割 $T=t_1+t_2+\cdots+t_k(k\geq 0)$满足:
分割中的每个串 $t_i$ 均为 $A$ 类串:即存在一个与其相等的 $A$ 类串,不妨假设其为 $t_i=A_{id_i}$。对于分割中所有相邻的串 $t_i,t_{i+1}(1\leq i<k)$,都有存在一个$A_{id_i}$ 支配的 $B$ 类串,使得该 $B$ 类串为 $t_{i+1}$ 的前缀。方便起见,你只需要输出这个最大的长度即可。
特别地,如果存在无限长的目标串(即对于任意一个正整数 $n$,都存在一个满足限制的长度超过 $n$ 的串),请输出 $-1$。
【输入格式】
单个测试点中包含多组数据,输入的第一行包含一个非负整数 $T$ 表示数据组数。接下来依次描述每组数据,对于每组数据:
第 1 行一个只包含小写字母的字符串 $S$。
第 2 行一个非负整数 $n_a$,表示 $A$ 类串的数目。接下来 $n_a$ 行,每行 2 个用空格隔开的整数。这部分中第 $i$ 行的两个数分别为 $la_i,ra_i$,描述第 $i$ 个 $A$ 类串。保证 $1\leq la_i\leq ra_i\leq |S|$。
接下来一行一个非负整数 $n_b$,表示 $B$ 类串的数目。接下来 $n_b$ 行,每行 2 个用空格隔开的整数。这部分中第 $i$ 行的两个数分别为 $lb_i,rb_i$,描述第$i$个 $B$ 类串。保证 $1\leq lb_i\leq rb_i\leq |S|$。
接下来一行一个非负整数 $m$,表示支配关系的组数。接下来 $m$ 行,每行 2 个用空格隔开的整数。这部分中每行的两个整数 $x,y$,描述一对 $(x,y)$ 的支配关系,具体意义见 【题目描述】。保证 $1\leq x\leq n_a,1\leq y\leq n_b$。保证所有支配关系两两不同,即不存在两组支配关系的 $x,y$ 均相同。
【输出格式】
依次输出每组数据的答案,对于每组数据:
一行一个整数表示最大串长。特别地,如果满足限制的串可以是无限长的,则请 输出$-1$。
【样例输入】
3 abaaaba 2 4 7 1 3 1 3 4 1 2 1 abaaaba 2 4 7 1 3 1 7 7 1 2 1 abbaabbaab 4 1 5 4 7 6 9 8 10 3 1 6 10 10 4 6 5 1 2 1 3 2 1 3 3 4 1
【样例输出】
7 -1 13
【样例说明】
对于第 1 组数据,A 类串有 aaba 与 aba,B 类串有 aa,且 $A_2$ 支配 $B_1$。我们可以找到串 abaaaba,它可以拆分成 $A_2 + A_1$,且 $A_1$ 包含由 $A_2$ 所支配的 $B_1$ 作为前缀。可以证明不存在长度更大的满足限制的串。
对于第 2 组数据,与第 1 组数据唯一不同的是,唯一的 $B$ 类串为 a。容易证明存在无限长的满足限制的串。
对于第 3 组数据,容易证明 abbaabbaaaabb 是最长的满足限制的串。
【数据规模与约定】
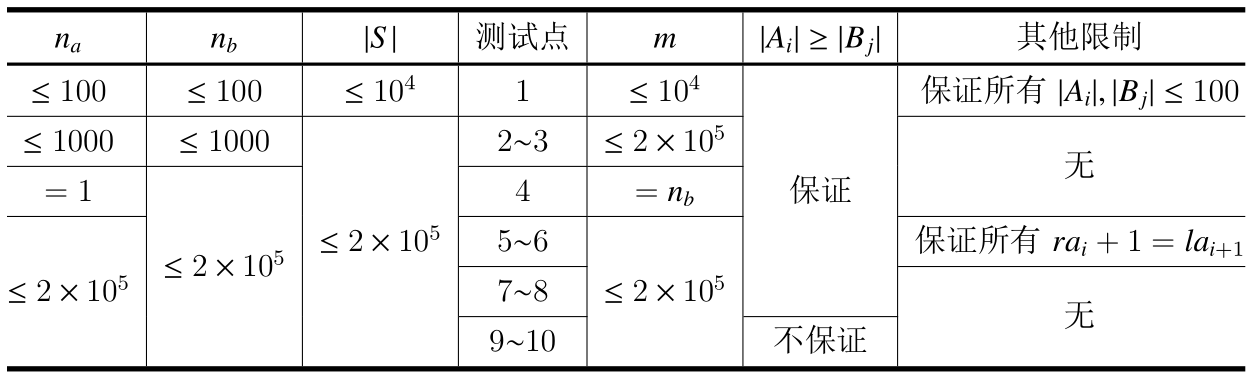
为了方便你的阅读,我们把测试点编号放在了表格的中间,请你注意这一点。
表格中的 $|A_i| > |B_j|$ 指的是任意 $B$ 类串的长度不超过任意 $A$ 类串的长度。
对于所有测试点,保证:$T\leq 100$,且对于测试点内所有数据,$|S|,n_a,n_b,m$的总和分别不会超过该测试点中对应的单组数据的限制的 10 倍。比如,对于第 1 组测试点,就有 $\sum{n_a}\leq 10\times 100=1000$等。特别地,我们规定对于测试点 4,有 $T\leq 10$。
对于所有测试点中的每一组数据,保证:$1 \leq |S| \leq 2 \times 10^5,n_a, n_b \leq 2 \times 10^5,m \leq 2 \times 10^5$。
【来源】
HAOI2019(12省联考)day1 T2