| 题目名称 | 4232. [NOIP 2025 T4]序列询问 |
|---|---|
| 输入输出 | query.in/out |
| 难度等级 | ★★★★☆ |
| 时间限制 | 3000 ms (3 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 20 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:2, 提交:3, 通过率:66.67% | ||||
|
|
100 | 23.914 s | 5.47 MiB | C++ |
|
|
100 | 28.582 s | 17.96 MiB | C++ |
|
|
15 | 54.406 s | 4.44 MiB | C++ |
| 关于 序列询问 的近10条评论(全部评论) |
|---|
【题目描述】
给定一个长度为 $n$ 的整数序列 $a_1, a_2, \ldots, a_n$。
有 $q$ 次询问,其中第 $j$ ($1 \le j \le q$) 次询问将会给出 $L_j, R_j$ ($1 \le L_j \le R_j \le n$)。定义区间 $[l, r]$ ($1 \le l \le r \le n$) 是极好的,当且仅当区间 $[l, r]$ 的长度在 $[L_j, R_j]$ 内,即 $L_j \le r - l + 1 \le R_j$。定义区间 $[l, r]$ ($1 \le l \le r \le n$) 的权值为 $\sum_{i=l}^{r} a_i$。对于所有 $i = 1, 2, \ldots, n$,求出所有包含 $i$ 的极好区间的最大权值,即 $\max_{1 \le l \le i \le r \le n} \{ \sum_{i=l}^{r} a_i \mid L_j \le r - l + 1 \le R_j \}$。
【输入格式】
输入的第一行包含一个正整数 $n$,表示序列长度。
输入的第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$。
输入的第三行包含一个正整数 $q$,表示询问次数。
输入的第 $j + 3$ ($1 \le j \le q$) 行包含两个正整数 $L_j, R_j$,表示第 $j$ 次询问。
【输出格式】
对于每次询问,设包含 $i$ ($1 \le i \le n$) 的极好区间的最大权值为 $k_i$,输出一行一个非负整数,表示 $\bigoplus_{i=1}^{n} \left( (i \times k_i) \bmod 2^{64} \right)$,其中 $\oplus$ 表示二进制按位异或。注意:对于任意整数 $x$,存在唯一的非负整数 $x'$ 满足 $x' \equiv x \pmod{2^{64}}$ 且 $0 \le x' \le 2^{64} - 1$,则记 $x \bmod 2^{64} = x'$。
【样例 1 输入】
4 2 4 -5 1 3 1 2 3 4 1 4
【样例 1 输出】
18446744073709551603 8 4
【样例 1 说明】
对于第 $1$ 次询问:
包含 $1$ 的极好区间为 $[1,1]$ 和 $[1,2]$,权值分别为 $2,6$;
包含 $2$ 的极好区间为 $[1,2]$,$[2,2]$ 和 $[2,3]$,权值分别为 $6,4,-1$;
包含 $3$ 的极好区间为 $[2,3]$,$[3,3]$ 和 $[3,4]$,权值分别为 $-1,-5,-4$;
包含 $4$ 的极好区间为 $[3,4]$ 和 $[4,4]$,权值分别为 $-4,1$。
因此 $k_1 = 6$,$k_2 = 6$,$k_3 = -1$,$k_4 = 1$。
对于第 2 次询问,$k_1 = 2$,$k_2 = 2$,$k_3 = 2$,$k_4 = 2$。
对于第 3 次询问,$k_1 = 6$,$k_2 = 6$,$k_3 = 2$,$k_4 = 2$。
【样例 2】
见选手目录下的 query/query2.in 与 query/query2.ans。
样例2满足测试点 $2,3$ 的约束条件。
【样例 3】
见选手目录下的 query/query3.in 与 query/query3.ans。
该样例满足测试点 $4$ 的约束条件。
【样例 4】
见选手目录下的 query/query4.in 与 query/query4.ans。
该样例满足测试点 $6,7$ 的约束条件。
【样例 5】
见选手目录下的 query/query5.in 与 query/query5.ans。
该样例满足测试点 $8 \sim 10$ 的约束条件。
【样例 6】
见选手目录下的 query/query6.in 与 query/query6.ans。
该样例满足测试点 $11,12$ 的约束条件。
【样例 7】
见选手目录下的 query/query7.in 与 query/query7.ans。
该样例满足测试点 $13$ 的约束条件。
【样例 8】
见选手目录下的 query/query8.in 与 query/query8.ans。
该样例满足测试点 $16 \sim 20$ 的约束条件。
【数据范围】
对于所有测试数据,均有:
$1 \le n \le 5 \times 10^4$,$1 \le q \le 1,024$;
对于所有 $1 \le i \le n$,均有 $|a_i| \le 10^5$;
对于所有 $1 \le j \le q$,均有 $1 \le L_j \le R_j \le n$。
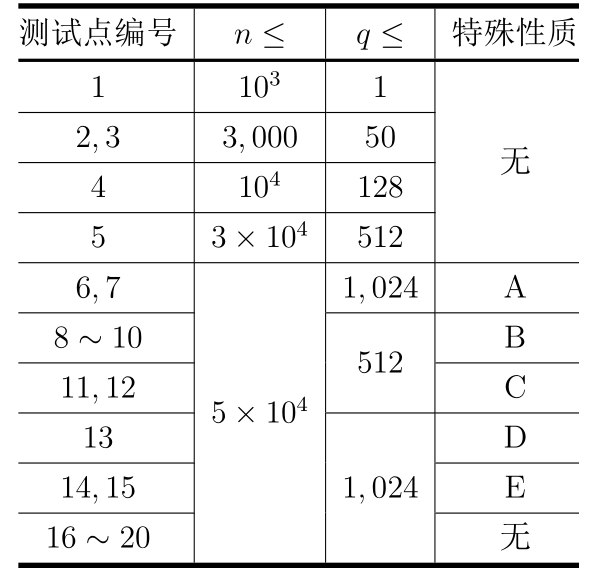
特殊性质 A:对于所有 $1 \le j \le q$,均有 $L_j = R_j$。
特殊性质 B:对于所有 $1 \le j \le q$,均有 $R_j \le 32$。
特殊性质 C:对于所有 $1 \le j \le q$,均有 $L_j \le 16$ 且 $R_j \ge n 1000$。
特殊性质 D:对于所有 $1 \le j \le q$,均有 $L_j > n/2$。
特殊性质 E:对于所有 $1 \le j \le q$,均有 $L_j > n/4$。