4110. t1

【题目描述】

观者有 $n$ 种姿态，初始她处于姿态 $1$。

接下来她会依次打出$n$ 张牌，牌一共有两种类型：

• 类型 $1$：直接将姿态变为 $x$；
• 类型 $2$：若姿态为$x$，将姿态转换为 $y$。

现在对于所有 $i\in [1,n]$，观者想知道她如果选择一些牌不打出（注意不能改变牌的顺序），最后能不能处于姿态 $i$，若可以，至少要跳过多少张牌？

【输入格式】

第一行一个正整数 $n$。

接下来 $n$  行，每行两至三个正整数表示一张牌，类型 $1$ 表示为 1 x，类型 $2$ 表示为 2 x y。

【输出格式】

一行 $n$  个数字，分别表示最后使得观者处于姿态$i$ 的代价，若不可能则输出 $-1$。

【样例输入】

4
1 1
1 2
2 2 3
2 1 4

【样例输出】

2 1 0 1

【样例说明】

样例1解释：

跳过第2、4张牌，最后姿态为1;

跳过第3张牌，最后姿态为2；

所有牌都不跳过，最后姿态为3;

跳过第2张牌，最后姿态为4.

大样例

【数据规模与约定】

对于 $100\%$ 的数据，保证 $2⩽n⩽10^6$，所有姿态编号在 $[1,n]$ 之间。

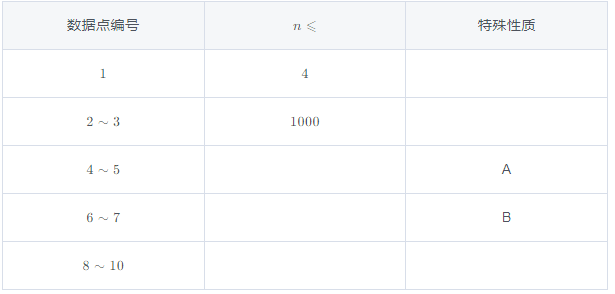
特殊性质 A：保证只存在类型 2。

特殊性质 B：保证所有类型 1 的牌在所有类型 2 的牌之前，即类型序列形如 1 1 1 ... 1 2 2 2 ... 2。

【来源】

核桃编程