| 题目名称 | 4231. [NOIP 2025 T3]树的价值 |
|---|---|
| 输入输出 | tree.in/out |
| 难度等级 | ★★★★☆ |
| 时间限制 | 2000 ms (2 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 25 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:1, 提交:2, 通过率:50% | ||||
|
|
100 | 6.025 s | 77.94 MiB | C++ |
|
|
0 | 3.507 s | 3.70 MiB | C++ |
| 关于 树的价值 的近10条评论(全部评论) |
|---|
【题目描述】
给定一棵 $n$ 个结点的有根树,其中结点 1 为根,结点 $i$ ($2 \le i \le n$) 的父亲结点为结点 $p_i$。
对于 $1 \le i \le n$,定义结点 $i$ 的深度 $d_i$ 为结点 1 到结点 $i$ 的简单路径的边数,也就是说,$d_1 = 0$,$d_i = d_{p_i} + 1$ ($2 \le i \le n$)。定义有根树的高度 $h$ 为所有结点的深度的最大值,即 $h = \max_{i=1}^{n} d_i$。
给定高度的上界 $m$。在本题中,给定的有根树的高度不超过 $m$。
你需要给每个结点设置一个非负整数作为它的权值。对于 $1 \le i \le n$,若结点 $i$ 的权值为 $a_i$,令 $S_i$ 表示结点 $i$ 的子树中结点权值构成的集合。对于每一种权值设置方案,定义树的价值为 $\sum_{i=1}^{n} \mathrm{mex}(S_i)$,其中 $\mathrm{mex}(S)$ 表示不在集合 $S$ 中的最小非负整数。例如,在下图中,若设置 $a_1 = 3$,$a_2 = 2$,$a_3 = a_4 = 0$,$a_5 = 1$,则 $S_1 = \{0,1,2,3\}$,$S_2 = \{0,1,2\}$,$S_3 = \{0\}$,$S_4 = \{0\}$,$S_5 = \{1\}$,树的价值为 $4 + 3 + 1 + 1 + 0 = 9$。
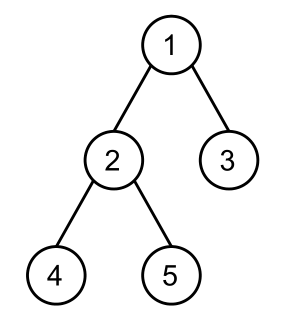
你需要求出,在所有权值设置方案中,树的价值的最大值。
【输入格式】
本题包含多组测试数据。
输入的第一行包含一个正整数 $t$,表示测试数据组数。
接下来依次输入每组测试数据,对于每组测试数据:
第一行包含两个正整数 $n, m$,分别表示结点数量与高度的上界。
第二行包含 $n-1$ 个正整数 $p_2, p_3, \ldots, p_n$,分别表示每个结点的父亲结点。
【输出格式】
对于每组测试数据,输出一行一个非负整数,表示树的价值的最大值。
【样例 1 输入】
2 5 2 1 1 2 2 7 2 1 1 2 2 2 3
【样例 1 输出】
9 13
【样例 1 说明】
该样例共包含两组测试数据。
对于第一组测试数据,可以设置 $a_1 = 3$,$a_2 = 2$,$a_3 = a_4 = 0$,$a_5 = 1$,则树的价值为 $4 + 3 + 1 + 1 + 0 = 9$。
对于第二组测试数据,可以设置 $a_1 = 4$,$a_2 = 3$,$a_4 = 2$,$a_3 = a_6 = 1$,$a_5 = a_7 = 0$,则树的价值为 $5 + 4 + 2 + 0 + 1 + 0 + 1 = 13$。
【样例 2】
见选手目录下的 tree/tree2.in 与 tree/tree2.ans。
该样例满足测试点 $3,4$ 的约束条件。
【样例 3】
见选手目录下的 tree/tree3.in 与 tree/tree3.ans。
该样例满足测试点 $7,8$ 的约束条件。
【样例 4】
见选手目录下的 tree/tree4.in 与 tree/tree4.ans。
该样例满足测试点 $13,14$ 的约束条件。
【样例 5】
见选手目录下的 tree/tree5.in 与 tree/tree5.ans。
该样例满足测试点 $18,19$ 的约束条件。
【数据范围】
对于所有测试数据,均有:
$1 \le t \le 5$;
$2 \le n \le 8,000$,$1 \le m \le \min(n-1, 800)$;
对于所有 $2 \le i \le n$,均有 $1 \le p_i \le i-1$;
给定的有根树的高度不超过 $m$。
