| 题目名称 | 4113. t4 |
|---|---|
| 输入输出 | emptymind.in/out |
| 难度等级 | ★★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 512 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:0, 提交:0, 通过率:0% | |||
| 本题关联比赛 | |||
| 2025新春开学欢乐赛 | |||
| 2025新春开学欢乐赛 | |||
| 关于 t4 的近10条评论(全部评论) |
|---|
【题目描述】
观者遇到一个发光立方体,这个立方体是一个 n 维的 Hypercube。
具体地,我们定义一个 n 维 Hypercube 是一张 2^n 个点的无向图,每个点编号为一个长为 n 的 01 串,两个点 u,v 之间有连边当且仅当 u,v 的 Hamming 距离为一,定义两个 01 串的 Hamming 距离为不相同的位数。
观者在这个 Hypercube 上画了三个高维球,第 i 个高维球的球心位于 s_i,半径为 r_i,这个高维球包含了所有满足 j 与 s_i 的 Hamming 距离不超过 r_i 的结点 j(容易发现 j 与 s_i 的 Hamming 距离即这两个结点在图上的最短路长度)。
她想知道,这三个球的并集包含多少结点。由于答案过大,你只需回答其对 10^9+7 取模的结果。
【输入格式】
第一行一个正整数 n。
接下来三行,每行一个长为 n 的 01 串 r_i 与一个正整数 s_i( 1⩽ i⩽ 3)。
【输出格式】
一行一个非负整数,表示答案。
【样例输入】
4 1 1101 2 0111 1 1001
【样例输出】
14
【样例说明】
在此键入。
【数据规模与约定】
对于 100% 的数据,2 ⩽ n ⩽ 6000, 0 ⩽ r_i ⩽ n-1。
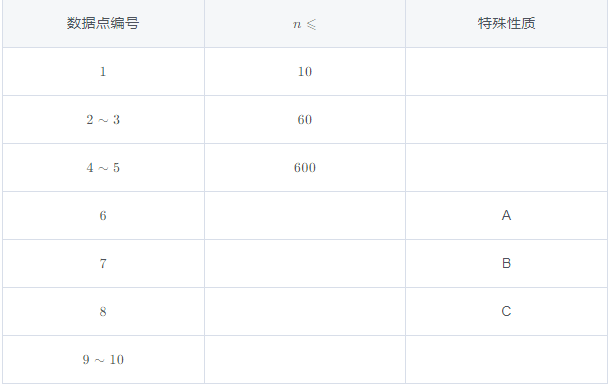
特殊性质 A:保证 s_1=s_2。
特殊性质 B:保证 r_1 ⩽ 5。
特殊性质 C:保证 s_1 与 s_2 恰好按位不同。
大样例【来源】
核桃编程