| 题目名称 | 2466. [CTSC 1997]选课 |
|---|---|
| 输入输出 | course.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 128 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:9, 提交:15, 通过率:60% | ||||
|
|
100 | 0.036 s | 4.20 MiB | C++ |
|
|
100 | 0.048 s | 1.84 MiB | C++ |
|
|
100 | 0.063 s | 4.09 MiB | C++ |
|
|
100 | 0.065 s | 4.30 MiB | C++ |
|
|
100 | 0.072 s | 4.11 MiB | C++ |
|
|
100 | 0.073 s | 4.78 MiB | C++ |
|
|
100 | 0.079 s | 5.20 MiB | C++ |
|
|
100 | 0.098 s | 4.62 MiB | C++ |
|
|
100 | 0.221 s | 4.52 MiB | C++ |
|
|
90 | 0.239 s | 4.08 MiB | C++ |
| 关于 选课 的近10条评论(全部评论) |
|---|
【题目描述】
大学里实行学分。每门课程都有一定的学分,学生只要选修了这门课并考核通过就能获得相应的学分。学生最后的学分是他选修的各门课的学分的总和。
每个学生都要选择规定数量的课程。其中有些课程可以直接选修,有些课程需要一定的基础知识,必须在选了其它的一些课程的基础上才能选修。例如,《数据结构》必须在选修了《高级语言程序设计》之后才能选修。我们称《高级语言程序设计》是《数据结构》的先修课。每门课的直接先修课最多只有一门。两门课也可能存在相同的先修课。为便于表述每门课都有一个课号,课号依次为 $1,2,3,……$。下面举例说明
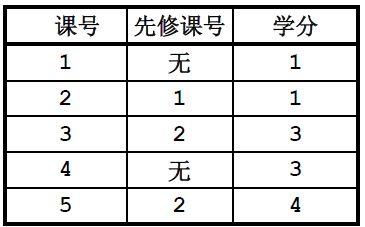
上例中 $1$ 是 $2$ 的先修课,即如果要选修 $2$,则 $1$ 必定已被选过。同样,如果要选修 $3$,那么 $1$ 和 $2$ 都一定已被选修过。
学生不可能学完大学所开设的所有课程,因此必须在入学时选定自己要学的课程。每个学生可选课程的总数是给定的。现在请你找出一种选课方案,使得你能得到学分最多,并且必须满足先修课优先的原则。假定课程之间不存在时间上的冲突。
【输入格式】
第一行包括两个正整数 $M、N$(中间用一个空格隔开)其中 $M$ 表示待选课程总数($1≤M≤500$),$N$ 表示学生可以选的课程总数($1≤N≤M$)。
以下 $M$ 行每行代表一门课,课号依次为 $1,2,…,M$。每行有两个数(用一个空格隔开),第一个数为这门课的先修课的课号(若不存在先修课则该项为 $0$),第二个数为这门课的学分。
【输出格式】
第一行只有一个数,即实际所选课程的学分总数。
【样例输入】
7 4 2 2 0 1 0 4 2 1 7 1 7 6 2 2
【样例输出】
13