| 题目名称 | 3614. 分配同桌 |
|---|---|
| 输入输出 | tongzhuo.in/out |
| 难度等级 | ★★☆ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:7, 提交:20, 通过率:35% | ||||
|
|
100 | 0.793 s | 30.37 MiB | C++ |
|
|
100 | 0.804 s | 20.25 MiB | C++ |
|
|
100 | 0.815 s | 20.25 MiB | C++ |
|
|
100 | 0.817 s | 20.25 MiB | C++ |
|
|
100 | 0.849 s | 30.37 MiB | C++ |
|
|
100 | 0.863 s | 20.25 MiB | C++ |
|
|
100 | 1.077 s | 30.37 MiB | C++ |
|
|
90 | 1.083 s | 30.37 MiB | C++ |
|
|
40 | 0.179 s | 20.25 MiB | C++ |
|
|
20 | 0.117 s | 20.25 MiB | C++ |
| 本题关联比赛 | |||
| 202110省实验桐柏一中普及组联赛 | |||
| 202110省实验桐柏一中普及组联赛 | |||
| 关于 分配同桌 的近10条评论(全部评论) |
|---|
【题目描述】
某班有若干个性格各异的大佬,大致可以分为外向的和内向的。为了使同学们相互学习,班主任决定重排座位,使尽量多对同桌的性格为一个外向一个内向,问最多可以安排几对这样的同桌。
同桌都是两两坐,因此每个人最多只能有$1$个同桌。
【输入格式】
输入文件有若干行:
第一行,两个整数$n$与$m$,表示共有$n$个同学$(10<=n<=10000)$,其中有$m$名同学是外向的;
接下来有若干行,每行有$2$个数字$a,b$。表示外向的$a$和内向的$b$可以坐同桌。(可能有重复)
注:外向的编号在前,且所有外向的编号都小于内向的编号,即外向的编号:$1$~$m$
内向的编号:$m+1$~$n$.
【输出格式】
输出文件有一行,包含$1$个整数,表示最多能匹配的同桌对数。
【样例输入】
10 5 1 6 1 8 2 6 3 6 3 7 4 8 4 9 4 10 4 10 5 8 5 9 [为了方便,样例数据从小到大给出,真实数据不一定如此]
【样例输出】
5
【样例说明】
如图中的$1,2,…,10$就代表$10$个同学,其中$1,2,3,4,5$是外向的,$6,7,8,9,10$是内向的。如果一个外向的同学和一个内向的同学可以做同桌,就在他们两个之间连一条线,两个人不能做同桌,就不连。注意:因为班主任很严格,两个外向的同学或两个内向的同学都一定不能做同桌.
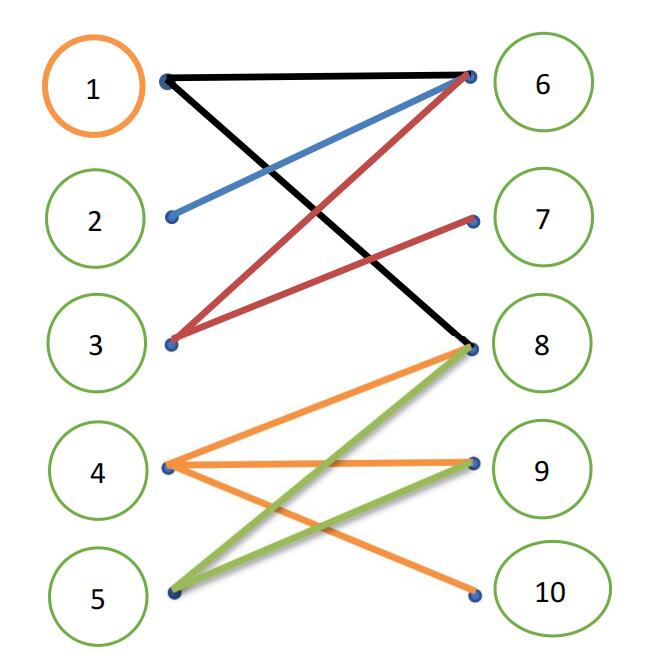
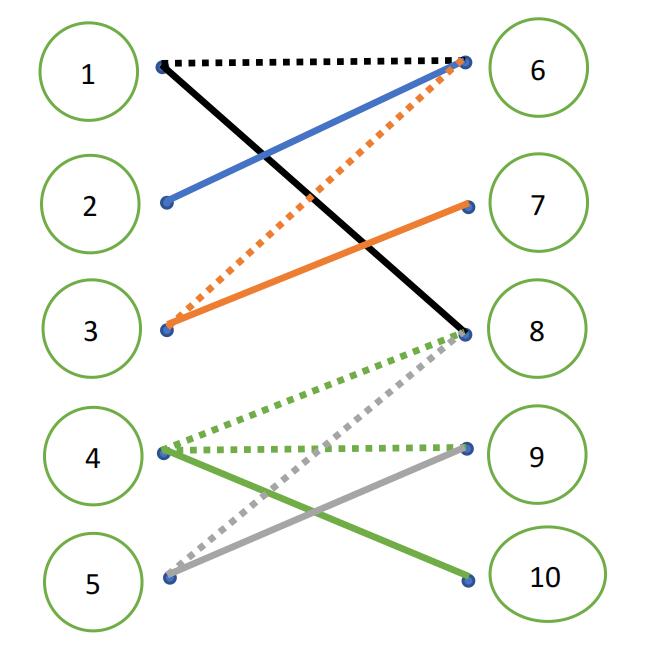
最大匹配方式可能不唯一,如图[实线表示匹配,虚线表示不匹配],一共匹配了$5$对同学,所有输出$5$。
【数据规模与约定】
$30$%的数据,$10<=n<=30;$
$50$%的数据,$10<=n<=50;$
$80$%的数据,$10<=n<=1000;$
$100$%的数据,$10<=n<=10000;$
【来源】
$dht@sywb$
$20211018$实验文博桐柏一中普及组联赛