| 题目名称 | 1481. [UVa 11426] 最大公约数之和——极限版II |
|---|---|
| 输入输出 | gcd_extreme.in/out |
| 难度等级 | ★★★☆ |
| 时间限制 | 5000 ms (5 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:106, 提交:247, 通过率:42.91% | ||||
|
|
100 | 0.479 s | 81.92 MiB | C++ |
|
|
100 | 0.640 s | 80.82 MiB | C++ |
|
|
100 | 0.854 s | 30.83 MiB | C++ |
|
|
100 | 0.894 s | 30.71 MiB | Pascal |
|
|
100 | 0.918 s | 70.58 MiB | C++ |
|
|
100 | 0.941 s | 85.46 MiB | C++ |
|
|
100 | 1.013 s | 30.68 MiB | Pascal |
|
|
100 | 1.025 s | 30.68 MiB | Pascal |
|
|
100 | 1.048 s | 65.17 MiB | C++ |
|
|
100 | 1.098 s | 30.68 MiB | Pascal |
| 关于 最大公约数之和——极限版II 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
回复 @Mike is Fool :
可以证明phi(T)= sigma ( d | T )u( T / d )* d
2017-01-03 20:21
18楼
| ||||
|
线性筛,隐式莫反(构造f函数的时候用的),分块,O(n)预处理,O(sqrt(n))查询
其中定义f(x)=(d|x)d*miu[x/d],不难证明f函数的积性,之后有假设1<=i,j<=n,ans=(1<=x<=n)(n/x)*(n/x)*f(x)(莫反的枚举变量交换一下),询问分块就好了。 不难证明,F(x)=(d|x)f(x)=x(莫比乌斯反演公式可证) 所以也可以杜教筛求f函数的前缀和,每次询问O(n^(2/3)),预处理O(n^(2/3))。 这真是智障,我用莫比乌斯函数求出来了欧拉函数- - | ||||
|
| ||||
|
单次O(输入的n)查询还是过了...
| ||||
|
欧拉函数前缀和
O(n)预处理 + O(sqrt(n))单次询问 | ||||
|
论大小号同时提交的后果......
然后...O(nlnn)的垃圾筛慢成翔啊......A不A全看评测机心情...... | ||||
|
O(n)做法
| ||||
|
模板就是硬
| ||||
|
回复 @<大神养成>溪哥 :
。。。。。。ORZ
2015-08-03 20:07
10楼
| ||||
|
样例更新了?好评!
| ||||
1481. [UVa 11426] 最大公约数之和——极限版II
★★★☆ 输入文件:gcd_extreme.in
输出文件:gcd_extreme.out
简单对比时间限制:5 s 内存限制:256 MiB
【题目描述】
输入正整数 $N$,求 $G$ 的值。$G$ 如下定义:
$G=\sum\limits_{i\in [1,N)}\sum\limits_{j\in[i+1,N]} \gcd(i,j)$
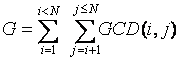
这里 $GCD(i,j)$ 代表 $i,j$ 的最大公约数。
对于不理解求和符号的人,下面给出了 $G$ 的代码表示:
G=0;
for(i=1;i<N;i++)
for(j=i+1;j<=N;j++)
{
G+=gcd(i,j);
}
/*gcd(i,j)的值是i,j的最大公约数*/
【输入格式】
输入包含至多 $100$ 组数据。每组数据占一行,包含正整数 $N(2 \leq N \leq 1 < N < 4000000)$。输入以 $N=0$ 结束。
【输出格式】
对于每组数据,输出一行,即所对应的 $G$ 值。答案保证在 $64$ 位带符号整数范围内。
【样例输入】
10 100 200000 0
【样例输出】
67 13015 143295493160
【提示】
对于 $30\%$ 的数据,$2 \leq N \leq 2000$
对于 $100\%$ 的数据,$2 \leq N \leq 4000000$
【来源】
刘汝佳,《算法竞赛入门经典训练指南》表2.4