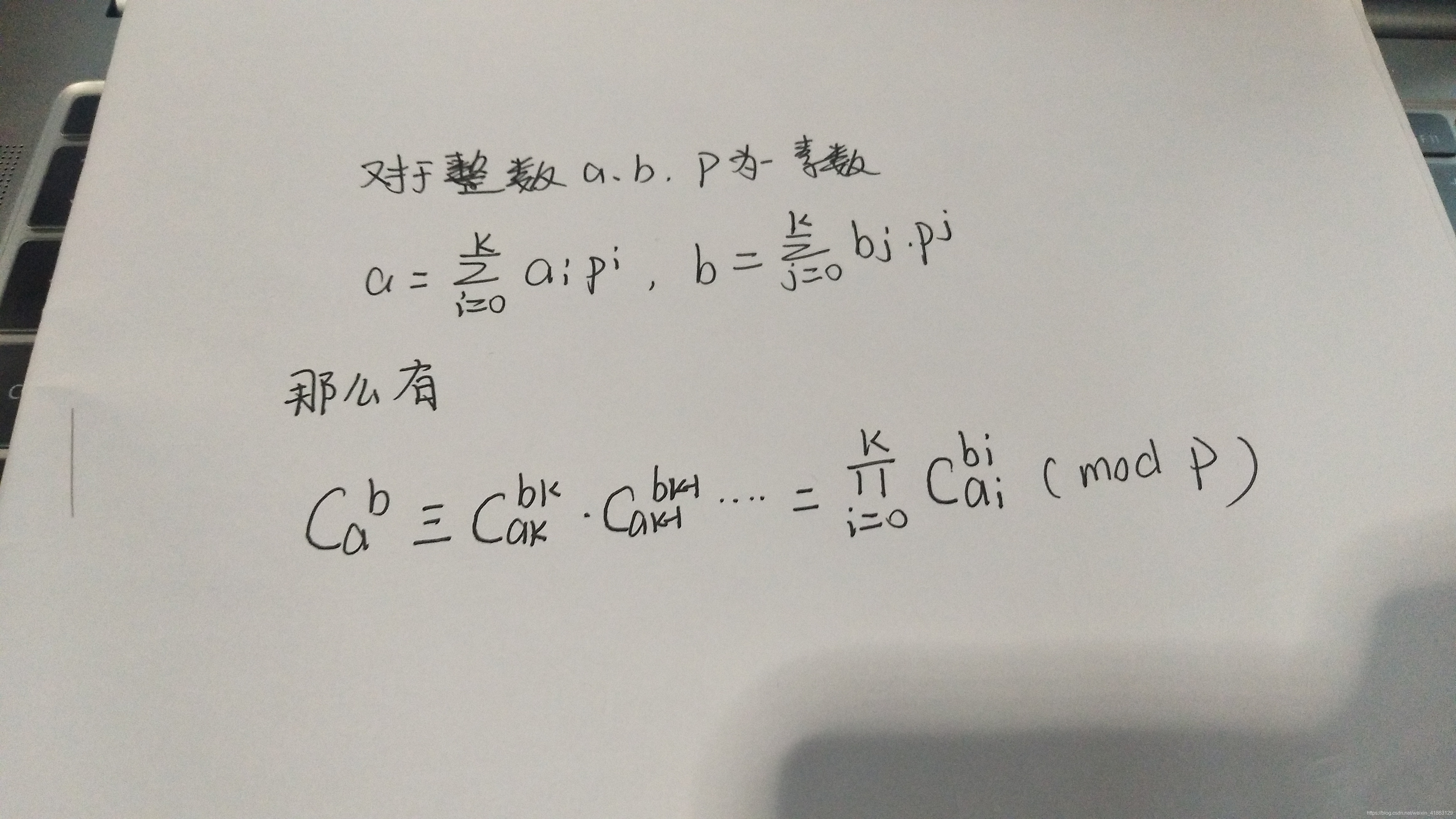COGS
-
- 0/1分数规划
- 01BFS
- 01背包
- 2-SAT
- A*
- ACM/ICPC
- AC自动机
- APIO
- BFS
- BFS序
- bitset 优化
- BSGS
- BYVoid
- CDQ分治
- COCI
- CodeChef
- Codeforces
- CTS论文相关
- DAG
- DFS
- DFS序
- DP套dp
- EZOI
- Fail树
- FFT
- FWT
- Gomory-Hu树
- HAOI
- HDU
- HEOI
- Hopcroft-karps算法
- hs的简单题
- HtBest
- HZOI
- IDA*
- IOI
- ISAP
- K-D Tree
- Keller系列
- KMP
- Kruskal 重构树
- K短路
- LCA
- LCP
- LCS
- LCT
- LIS
- Lucas定理
- Meet in the Middle算法
- NOI
- NOIP/CSP
- NP问题
- NTT
- POJ
- Polya 定理
- polya罐子模型
- RMQ
- SDOI
- SG函数
- Splay
- SPOJ
- ST表
- SYOI
- TopCoder
- Ural
- USACO
- UVa
- ZJOI
- 埃氏筛
- 半平面交
- 保序回归问题
- 背包类树形DP
- 背包问题
- 倍增法
- 表达式求值
- 表达式树
- 并查集
- 博弈论
- 插头DP
- 差分
- 差分约束
- 长链剖分
- 乘法逆元
- 乘法原理
- 次短路
- 次小生成树
- 带花树
- 带权并查集
- 带修莫队
- 单纯形
- 单调队列
- 单调栈
- 倒序处理
- 狄利克雷前缀和
- 递归
- 递推
- 点分治
- 点双连通分量
- 迭代加深搜索
- 动态规划
- 动态开点
- 动态树
- 动态图
- 杜教筛
- 堆
- 队列
- 对偶图
- 多项式求逆
- 多重背包
- 二叉树
- 二分答案
- 二分法
- 二分图
- 二分优化
- 二维偏序
- 二维树状数组
- 二维线段树
- 二项式定理
- 反图
- 斐波那契数列
- 分层图
- 分块
- 分形
- 分治
- 分组背包
- 浮点运算
- 浮水法
- 复杂度分析
- 概率分析
- 概率与期望
- 高等数学
- 高精度
- 高精快速幂
- 高斯消元法
- 割点与桥
- 根号分治
- 构造
- 估价函数
- 滚动数组
- 哈夫曼树
- 合并类动态规划
- 黑白染色
- 后效性
- 后缀树
- 后缀数组
- 后缀自动机
- 划分树
- 换根
- 回溯法
- 回文
- 回文自动机
- 基本
- 基环树
- 基环树DP
- 集合幂级数
- 计数
- 计数类DP
- 计算几何
- 记忆化搜索
- 剪枝
- 交互式
- 结构体
- 结论
- 解异或方程组
- 局部搜索
- 矩阵乘法
- 矩阵快速幂
- 矩阵树定理
- 矩阵运算
- 决策单调性优化
- 卡特兰数
- 可持久化
- 可持久化平衡树
- 可持久化线段树
- 快速幂
- 扩展欧几里得算法
- 括号匹配
- 拉格朗日插值
- 勒让德定理
- 类背包
- 离散化
- 李超线段树
- 连通分量
- 连通性
- 链分治
- 轮廓线DP
- 洛谷
- 枚举
- 密码
- 模拟
- 模拟退火
- 模式匹配
- 模线性方程组
- 模型转换
- 莫比乌斯反演
- 莫队
- 母函数/生成函数
- 拟阵
- 逆序对
- 欧几里得算法
- 欧拉定理及扩展
- 欧拉反演
- 欧拉函数
- 欧拉路径
- 欧拉筛法
- 排列组合
- 排序
- 平衡树
- 平面图
- 瓶颈生成树
- 启发式合并
- 前缀和
- 强连通分量
- 清北学堂
- 区间DP
- 群论
- 人工智能
- 容斥原理
- 三分法
- 三维莫队
- 三维偏序
- 散列
- 扫描线法
- 生物
- 树
- 树的直径
- 树的重心
- 树分块
- 树分治
- 树链剖分
- 树上差分
- 树套树
- 树形DP
- 树状数组
- 数据结构优化建图
- 数论
- 数位DP
- 数学
- 数值方法
- 双端队列
- 双连通分量
- 双向BFS
- 双向DFS
- 双向DP
- 双指针扫描法
- 思维
- 斯特林数
- 四叉树
- 四分树
- 搜索法
- 素数筛法
- 随机化
- 缩点
- 贪心
- 特判
- 特殊判断
- 替罪羊树
- 同余
- 凸包
- 凸轮
- 图的匹配
- 图论
- 拓扑排序
- 完全背包
- 网络流
- 位运算
- 文法分析
- 物理
- 稀疏表
- 仙人掌图
- 弦图
- 弦图和区间图
- 线段树
- 线段树分治
- 线段树合并
- 线性DP
- 线性规划
- 线性基
- 线性结构
- 线性空间
- 斜率优化
- 匈牙利算法
- 虚树
- 悬线法
- 压位
- 异或相关
- 映射
- 优先队列
- 有限状态自动机
- 圆方树
- 栈
- 找规律
- 折半递归
- 整体二分
- 整体分治
- 支配树
- 中国剩余定理
- 种子填充
- 重链剖分
- 主元素问题
- 状态压缩
- 状压DP
- 子集和变换
- 字典树/Trie
- 字符串
- 字符串哈希
- 字符串排序
- 自然数拆分问题
- 组合数学
- 最大公约数
- 最短路
- 最短路径树
- 最小表示法
- 最小割
- 最小割树
- 最小公倍数
- 最小生成树
- 最值子图
- 左偏树
- 题目
- 题解
- 记录
- 比赛
- 页面
- 用户
- 评论
|
|
前置知识 $Lucas$ 定理,中国剩余定理($CRT$),费马-欧拉定理。 费马-欧拉定理 设 $a,m$ ∈ $N^+$,且 $gcd$($a,m$)= $1$,则我们有: $a^φ$≡$1$($/mod m$)。 其中,φ($m$) 称为对模 $m$ 缩系的元素个数。 此外,$a$ 对模 $m$ 的阶必整除 $φ$($m$)。
证明如下:(自己度娘) https://baike.baidu.com/item/%E6%AC%A7%E6%8B%89%E5%AE%9A%E7%90%86/891345 Lucas定理
中国剩余定理(CRT)
题面概述 存在一个整数 $N$,对于约数$d$($d|N$),求 $C_d^n$ 对 $999911659$ 取模的值
思路 $O(N)$预处理,$O(1)$查询: 先求出模 $p$ 意义下的阶乘,逆元以及逆元阶乘(因为求逆元满足积性函数)。 对于任意一个小于p的组合数 $C_m^n$,可以直接用 $jc[m] /times invjc[n] /times invjv[m-n]求出,其中 $jc[i]$ 指到 $i$ 的阶乘, $invjc[i]$ 指到 $i$ 的阶乘逆元
代码就不贴了…… 0ms,0Mid
2022-08-07 10:16:22
|