|
|
突然发现自己暑假写过这题。 显然可以考虑动态规划,但不难发现用时间做状态没前途,用站点做状态转移比较困难,而用车次做转移刚刚好。 设 $f_i$ 表示坐上列车 $i$ 的最小烦躁值,因为并没有保证 $x_i<y_i$,所以转移的顺序要按照 $p$ 来排,每次要转移的来源必须满足 $y_j=x_i,q_j\le p_i$。不难完成 $O(n^2)$ 的代码。 考虑优化,注意到转移很像斜率优化,所以使用李超线段树,每次计算完 $f_i$ 后,将 $(q_i,i)$ 放入二叉堆按 $q_i$ 排序。每次转移前,取出二叉堆中所有满足 $q_j\le p_i$ 的 $j$,然后将直线 $j$ 插入第 $y_j$ 个位置的李超树。 李超树动态开点空间复杂度 $O(n)$,时间复杂度 $O(n\log V)$。
题目3224 [NOI 2019]回家路线
AAAAAAAAAAAAAAAAAAAA
评论
2026-02-25 13:29:09
|
|
|
更好的阅读体验https://www.cnblogs.com/To-Carpe-Diem/p/19635184
大意 给出 $b_{i, j} = a_{i - 1, j} + a_{i, j - 1} + a_{i - 1, j - 1} + a_{i, j}$,要求给出一组 $a$ 的可行解,保证 $0 \le a_{i, j} \le 10 ^ 6$。
思路 这集真的神了。 我们想一个问题,首先这个题我们很容易构造出一个 $a$,使其满足 $b$ 的性质,我们将 $a_{i, 1}$ 和 $a_{1, i}$ 都设为 $0$,那么我们有这样的转移式子:$a_{i, j} = b_{i - 1, j - 1} - a_{i - 1, j} - a_{i, j - 1} - a_{i - 1, j - 1}$,这样构造出来的 $a$ 是含有负数的,但是我们考虑进行调整。 这里有一个小巧思,我们考虑对于每一行和每一列进行增量的操作,加减交替,这样会得到以下这个样子的矩阵: $\begin{pmatrix}r_1 + c_1 & -r_1 + c_2 & r_1 + c_3 & \cdots \\r_2 - c_1 & -r_2 - c_2 & r_2 - c_3 & \cdots \\r_3 + c_1 & -r_3 + c_2 & r_3 + c_3 & \cdots \\\vdots & \vdots & \vdots & \ddots\end{pmatrix}$ 有什么用呢???我们发现 $(r_1 + c_1) + (-r_1 + c_2) + (r_2 - c_1) + (-r_2 - c_2) = 0$,那么这样我们就在不改变 $b$ 的情况下可以对 $a$ 进行调整,那么会变成类似于这样的差分约束系统:$0 \le a_{i, j} \pm r_i \pm c_i \le 10 ^ 6$,我们就直接对这样的建立差分约束系统,然后跑 SPFA 即可(注意判负环,如果有负环说明就没有答案)
代码
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
const int MAXN = 1005;
const int INF = 1000000;
int T;
int n, m;
int b[MAXN][MAXN];
int a[MAXN][MAXN];
vector<pair<int, int> > g[MAXN];
bool vis[MAXN << 1];
int dis[MAXN << 1], in[MAXN << 1];
queue<int> q;
void init(){
while(!q.empty()) q.pop();
for(int i = 1;i <= n + m;i ++){
dis[i] = 0;
vis[i] = 1;
in[i] = 0;
q.push(i);
}
}
void solve(){
cin >> n >> m;
for(int i = 1;i < n;i ++){
for(int j = 1;j < m;j ++){
cin >> b[i][j];
}
}
for(int i = 1;i <= n;i ++)
for(int j = 1;j <= m;j ++)
a[i][j] = 0;
for(int i = 2;i <= n;i ++){
for(int j = 2;j <= m;j ++){
a[i][j] = b[i - 1][j - 1] - a[i - 1][j] - a[i][j - 1] - a[i - 1][j - 1];
// cout << a[i][j] << ' ';
}
// cout << endl;
}
for(int i = 1;i <= n + m + 1;i ++) g[i].clear();
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= m;j ++){
if((i + j) & 1){
g[i].push_back(make_pair(j + n, a[i][j]));
g[j + n].push_back(make_pair(i, INF - a[i][j]));
}
else{
g[j + n].push_back(make_pair(i, a[i][j]));
g[i].push_back(make_pair(j + n, INF - a[i][j]));
}
}
}
init();
while(!q.empty()){
int u = q.front(); q.pop(); vis[u] = 0;
for(auto x : g[u]){
int v = x.first, w = x.second;
if(dis[u] + w < dis[v]){
dis[v] = dis[u] + w;
if(!vis[v]){
in[v] ++;
if(in[v] > n + m + 1){
cout << "NO\n";
return;
}
vis[v] = 1;
q.push(v);
}
}
}
}
bool flag = 1;
// cout << "YES\n";
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= m;j ++){
if((i + j) & 1) a[i][j] += (dis[i] - dis[j + n]);
else a[i][j] += (dis[j + n] - dis[i]);
if(a[i][j] < 0) flag = 0;
// cout << a[i][j] << ' ';
}
// cout << '\n';
}
if(flag){
cout << "YES\n";
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= m;j ++){
cout << a[i][j] << ' ';
}
cout << '\n';
}
}
else cout << "NO\n";
}
int main(){
// freopen("matrix.in", "r", stdin);
// freopen("matrix.out", "w", stdout);
cin.tie(0) -> ios::sync_with_stdio(0);
cin >> T;
while(T --){
solve();
}
return 0;
}
题目3580 [统一省选 2021]矩阵游戏
AAAAAAAAAAAAAAAAAAAA
评论
2026-02-24 21:20:32
|
|
|
更好的阅读体验:https://www.cnblogs.com/To-Carpe-Diem/p/19635135
大意 求前 $k$ 大的互不相同的异或和。
思路 首先,我们将其转换一下,求出前缀异或和,$s$,$s_i = s_i \oplus s_{i - 1} $,这样,对于区间 $[l, r]$ 的异或和询问就变成了 $s_r \oplus s_{l - 1}$。 知道了这个之后,我们的问题现在转化为了,在这 $n$ 个 $s$ 里面选择 $k$ 对,使得其和最大,这个时候,我们要处理的问题是对于 $s_i$ 来说,如何找到一个 $s_j$,使得其 $s_i \oplus s_j$ 的值最大。这个问题十分经典(但是我也刚知道),可以用 Trie 来处理这种动态找最大异或和的问题。 那么如何在 Trie 上维护这个东西呢?我们考虑将每个 $s_i$ 插入 Trie 里面,那么记录每个节点经过的点的个数,我们一定是希望走 $op \oplus 1$ 的位置的,但是如果没有 $op \oplus 1$ 这个位置,就走不了,且,若是左子树的大小不够,也走不了,必须走到 $sz \ge rk$ 的地方,这个才是对的。于是就类似权值线段树静态查第 $k$ 大差不多,不过此题我们要处理的是前 $2k$ 大,因为我们忽略了 $l \le r$ 的限制。 我们只需要用一个大根堆记录即可,但是每个答案都会以 $s_i$ 和 $s_j$ 为基准分别各出现一次,那么最终我们选择的答案需要除以 $2$。
代码
#include<iostream>
#include<queue>
using namespace std;
#define ll long long
const int MAXN = 5e5 + 5;
const int MAXT = MAXN * 32;
int ch[MAXT][2], cnt[MAXT];
ll s[MAXN], tot = 0, n, k;
struct node{
int id, rk;
ll val;
bool operator<(const node &other)const{
return val < other.val;
}
};
void Insert(ll x){
int now = 0;
for(int i = 31;i >= 0;i --){
int op = (x >> i) & 1;
if(!ch[now][op]) ch[now][op] = ++ tot;
now = ch[now][op];
cnt[now] ++;
}
}
ll query(ll x, int rk){
int now = 0;
ll res = 0;
for(int i = 31;i >= 0;i --){
int op = (x >> i) & 1;
op ^= 1;
if(!ch[now][op]){
now = ch[now][op ^ 1];
}
else if(rk <= cnt[ch[now][op]]){
res |= (1LL << i);
now = ch[now][op];
}
else{
rk -= cnt[ch[now][op]];
now = ch[now][op ^ 1];
}
}
return res;
}
int main(){
cin.tie(0) -> ios::sync_with_stdio(0);
cin >> n >> k;
s[0] = 0;
Insert(s[0]);
for(int i = 1;i <= n;i ++){
ll a; cin >> a;
s[i] = s[i - 1] ^ a;
Insert(s[i]);
}
priority_queue<node> q;
for(int i = 0;i <= n;i ++){
ll x = query(s[i], 1);
q.push({i, 1, x});
}
ll ans = 0;
for(int i = 1;i <= 2 * k;i ++){
node t = q.top();
ans += t.val;
q.pop();
if(t.rk < n){
q.push({t.id, t.rk + 1, query(s[t.id], t.rk + 1)});
}
}
cout << ans / 2;
return 0;
}
题目3103 [HAOI 2019]异或粽子
AAAAAAAAAAAAAAAAAAAA
评论
2026-02-24 20:48:23
|
|
|
更好的阅读体验:https://www.cnblogs.com/To-Carpe-Diem/p/19635009
大意 给出 $n$ 张卡牌,每张卡牌都有两个权值 $a_i$ 和 $b_i$,分别对应的是正面和反面,求在至少翻 $m$ 张牌,然后求出最小的极差。
思路 我们考虑这样的事,首先,我们不考虑每一张牌的情况,我们只考虑这个先处理极差的问题,我们先把这 $2n$ 张牌记录一下类型,然后将其排序。 排完序之后,我们需要的是选择一段区间 $[L, R]$,使得 $[L, R]$ 的区间包含所有的类型,且其中间反转的牌不超过 $m$ 个,那么这个区间的 $val_R - val_L$ 就是一个合法的答案,我们要想使得这个值尽可能的小,我们不妨使用双指针的写法,固定左端点,向右查询合法右端点。 这个过程是具有单调性的,你的 $L$ 向右,$R$ 也必定向右,具体过程是这样的,如果当前的区间不合法,那么就让 $R$ 右移,使其包含所有的 $n$ 个情况,一旦包含足够,就判断是否合法,这个过程是可以在扫描的过程中动态处理的,这步判断是 $\mathcal{O}(1)$ 的,如果是合法就将 $L$ 向右收缩,这样去看看有没有更优的 $val_R - val_L$。
代码
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 1e6 + 5;
int n, m, l, r, cnt = 0;
struct node{
long long val, id;
bool op;
}k[MAXN << 1];
int t[MAXN << 1];
bool cmp(node x, node y){
return x.val < y.val;
}
int main(){
// freopen("card.in", "r", stdin);
// freopen("card.out", "w", stdout);
cin.tie(0) -> ios::sync_with_stdio(0);
cin >> n >> m;
for(int i = 1;i <= n;i ++){
cin >> k[i].val;
k[i].id = i;
k[i].op = 1;
}
for(int i = 1;i <= n;i ++){
cin >> k[i + n].val;
k[i + n].id = i;
k[i + n].op = 0;
}
sort(k + 1, k + 2 * n + 1, cmp);
// for(int i = 1;i <= n * 2;i ++){
// cout << k[i].val << ' ' << k[i].id << ' ' << k[i].op << '\n';
// }
for(l = 0;cnt + k[l + 1].op <= m && !t[k[l + 1].id];l ++){
cnt += k[l + 1].op;
t[k[l + 1].id] = 1;
}
for(r = 2 * n + 1;cnt + k[r - 1].op <= m && !t[k[r - 1].id];r --){
cnt += k[r - 1].op;
t[k[r - 1].id] = 1;
}
long long ans = 1e9 + 7;
while(l >= 0) {
ans = min(k[r - 1].val - k[l + 1].val, ans);
t[k[l].id] = 0;
cnt -= k[l].op;
l --;
for(r;cnt + k[r - 1].op <= m && !t[k[r - 1].id];r --){
cnt += k[r - 1].op;
t[k[r - 1].id] = 1;
}
}
cout << ans << '\n';
}
题目3579 [统一省选 2021]卡牌游戏
AAAAAAAAAA
评论
2026-02-24 20:22:45
|
|
|
更好的阅读体验:https://www.cnblogs.com/To-Carpe-Diem/p/19635050
大意 给定一个序列,每个数有两种颜色,要找到一个位置,要找到一个位置使得 $\min \{ f(p), g(p) \}$ 尽可能大.
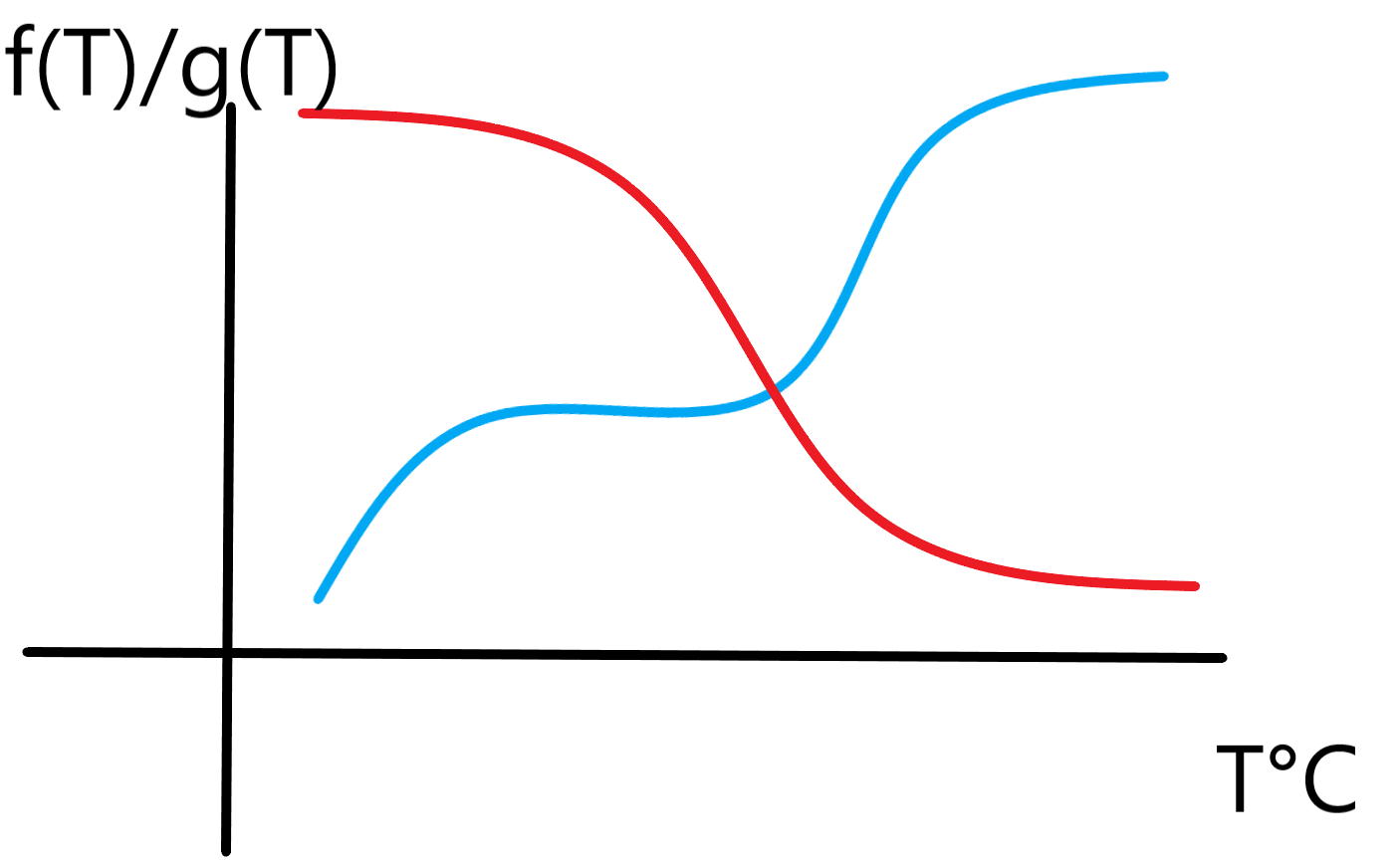
思路 我们在温度 $T$ 下,能参加的冰人必须是 $y \le T$ 的才能参赛,火人必须是 $y \ge T$ 才能参赛,我们定义能参赛的冰人的能量和为 $f(T)$,同理,火人为 $g(T)$。 那么我们的答案一定是 $2 \times \min \{ f(T), g(T)\}$,对于这个图,画出来是下面这样的:
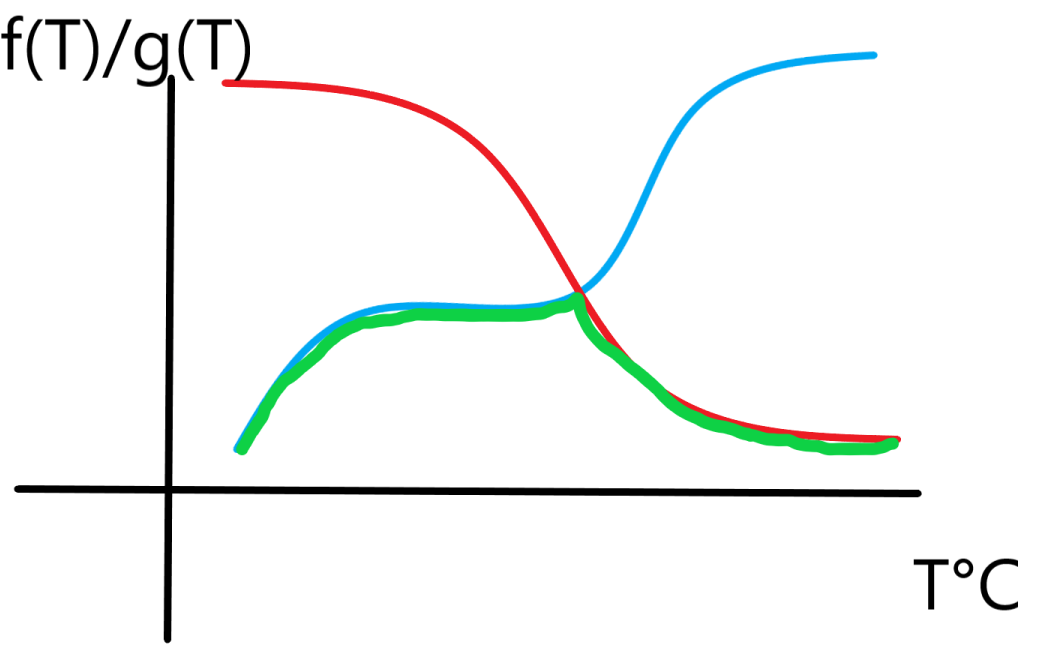
那么,取 $\min$ 之后的图像是这样的:
就是绿色的部分,那么我们这样的话,答案一定在交点附近,那么我们在求这个交点的过程,可以尝试二分 + 树状数组,由于一个是递增,一个是递减,分别维护前缀和和后缀和即可,那么这样二分到交点 $p$ 的话,只需要看 $p$ 和 $p + 1$ 位置,相当于是冰人和火人的位置,火人的位置比较特殊,因为是可能后面还有段连续的区间,需要继续从 $p + 1$ 向右跳到最后一个合法的区间。 而上述的做法,不难发现时间复杂度是 $Q \log^2 Q$ 的,无法通过此题,只能有 $60pts$,于是我们考虑优化。 有个比较经典的思路(不过我也是刚学会的),在树状数组上倍增,这样的话,我们只需要单 $\log$ 的复杂度去跳交点,以及查找 $p + 1$ 的后面最后一个满足情况的点即可。
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXN = 2 * 1e6 + 5;
ll t1[MAXN], t2[MAXN];
int lsh[MAXN], tot;
ll sum = 0;
struct node{
int op, t, x, y;
}q[MAXN];
int lowbit(int x){
return x & -x;
}
void add(ll *bit, int x, ll k){
// if(x <= 0) return;
while(x <= tot + 1){
bit[x] += k;
x += lowbit(x);
}
}
int Q;
int main(){
cin.tie(0) -> ios::sync_with_stdio(0);
cin >> Q;
for(int i = 1;i <= Q;i ++){
cin >> q[i].op;
if(q[i].op == 1){
cin >> q[i].t >> q[i].x >> q[i].y;
lsh[++ tot] = q[i].x;
}
else{
cin >> q[i].t;
}
}
sort(lsh + 1, lsh + tot + 1);
tot = unique(lsh + 1, lsh + tot + 1) - (lsh + 1);
for(int i = 1;i <= Q;i ++){
if(q[i].op == 1){
q[i].x = lower_bound(lsh + 1, lsh + tot + 1, q[i].x) - lsh;
}
}
for(int i = 1;i <= Q;i ++){
if(q[i].op == 1){
if(q[i].t == 0) add(t1, q[i].x, q[i].y);
else add(t2, q[i].x + 1, q[i].y), sum += q[i].y;
}
else{
if(q[q[i].t].t == 0) add(t1, q[q[i].t].x, -q[q[i].t].y);
else add(t2, q[q[i].t].x + 1, -q[q[i].t].y), sum -= q[q[i].t].y;
}
ll p1 = 0, s1 = 0, s2 = 0;
for(int j = 20;j >= 0;j --){
int nxt = p1 + (1 << j);
if(nxt <= tot && s1 + t1[nxt] < sum - (s2 + t2[nxt])){
p1 = nxt, s1 += t1[nxt], s2 += t2[nxt];
}
}
ll res1 = s1;
ll res2 = 0, p2 = 0;
if(p1 < tot){
ll ss1 = 0, ss2 = 0;
for(int j = p1 + 1;j;j -= lowbit(j)){
ss1 += t1[j], ss2 += t2[j];
}
res2 = sum - ss2;
if(res2 >= res1){
p2 = 0, ss2 = 0;
for(int j = 20;j >= 0;j --){
int nxt = p2 + (1 << j);
if(nxt <= tot && sum - (ss2 + t2[nxt]) >= res2){
p2 = nxt;
ss2 += t2[nxt];
}
}
}
}
if(res1 == res2 && res1 == 0){
cout << "Peace\n";
}
else if(res1 <= res2){
cout << lsh[p2] << ' ' << res2 * 2 << '\n';
}
else{
cout << lsh[p1] << ' ' << res1 * 2 << '\n';
}
}
return 0;
}
题目3417 [统一省选 2020]冰火战士
AAAAAAAAAA
评论
2026-02-24 20:22:10
|
|
|

题目3579 [统一省选 2021]卡牌游戏
AAAAAAAAAA
评论
2026-02-24 14:53:05
|