|
|
#include<bits/stdc++.h>
using namespace std;
string s1,s2;
int a[250],b[250],c[250];
char f = '+';
int len,p;
int main(){
freopen("sub.in","r",stdin);
freopen("sub.out","w",stdout);
cin >> s1 >> s2;
if (s2.size() > s1.size() || (s1.size() == s2.size() && s2 > s1)) {
swap(s1,s2);
f = '-';
}
for (int i = 0; i < s1.size(); i++) {
a[s1.size() - i - 1] = s1[i] - '0';
}
for (int i = 0; i < s2.size(); i++) {
b[s2.size() - i - 1] = s2[i] - '0';
}
len = s1.size();
for (int i = 0; i < len; i++) {
if (a[i] < b[i]) {
a[i + 1] -= 1;
a[i] += 10;
}
c[i] = a[i] - b[i];
}
if (f == '-') cout << f;
for (int i = len - 1; i >= 0; i--) {
if (c[i] != 0) {
p = i;
break;
}
}
for (int i = p; i >= 0; i--) cout << c[i];
}
这道题用三个数组就行。 第一步:把输入的字符串转换成数组(因为都是数字) 第二步:相减,不够就借位 第三步:判断是否是负数 第四步:输出
题目38 增强的减法问题
AAAAAAAAAA
 3
评论 3
评论
2022-11-07 09:52:51
|
|
|
Pro3790 界外科学 题解本题三种做法。 第一种:直接跑一遍dfs求最大值,期望得分50分。 第二种:折半搜索,map统计去重,最后求最大值。
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n, m, half, a[50], b[50], num1[1 << 21], num2[1 << 21], cnt1, cnt2, ans;
map<int, int> mp, mp2;
int dfs2(int x, int s, int p) {
if(x == n + 1) {
if(!mp2[p]) {
num2[++ cnt2] = p;
}
if(s > mp2[p]) {
mp2[p] = s;
}
return 0;
}
dfs2(x + 1, s, p);
dfs2(x + 1, s + b[x], p ^ a[x]);
}
int dfs(int x, int s, int p) {
if(x == half + 1) {
if(!mp[p]) {
num1[++ cnt1] = p;
}
if(s > mp[p]) {
mp[p] = s;
}
return 0;
}
dfs(x + 1, s, p);
dfs(x + 1, s + b[x], p ^ a[x]);
return 0;
}
signed main() {
freopen("outsci.in", "r", stdin);
freopen("outsci.out", "w", stdout);
cin >> n >> m;
half = n / 2;
for(int i = 1; i <= n; i ++) {
cin >> a[i];
}
for(int i = 1; i <= n; i ++) {
cin >> b[i];
}
dfs(1, 0, 0);
// for(int i = 1; i <= cnt; i ++) {
// cout << c[i] << ' ' << mp[c[i]] << endl;
// }
dfs2(half + 1, 0, 0);
for(int i = 1; i <= cnt1; i ++) {
for(int j = 1; j <= cnt2; j ++) {
if((num1[i] ^ num2[j]) <= m) {
ans = max(ans, mp[num1[i]] + mp2[num2[j]]);
}
}
}
cout << ans << endl;
return 0;
}
第三种 正解(伪):所有大于零的b求和( 这数据是拿脚捏的吗?这都能水过??? 真正的正解还没想到QAQ
题目3790 界外科学
WWWWWWWWWWWW
 10
评论 10
评论
2022-11-06 21:22:10
|
|
|
当大家都在写线段树时,我在写分块( 这题求的是交替序列值,正常的是求区间和,那么我们如何转换区间和为交替序列值呢? 我们可以将序列分为两部分,下标为 $i$ 的数 $a_i$ 属于第 $i%2$ 个部分。那么我们就将序列拆为了两部分,其中用第 $0$ 部分序列和减去第 $1$ 部分的序列和即为交替序列值。 但是上面的情况只适用于 $l%2=1$ 的情况,另一种情况取个相反数就行了。
题目2951 [SYOI 2018] WHZ 的序列
AAAAAAAAAA
 10
评论 10
评论
2022-11-06 21:15:29
|
|
|
先吐槽下COGS评测机,洛谷AC,这里不开O2会T( 以下转载于我的洛谷博客:
赛场切了很开心,于是写篇题解。
看到题后我们可以想一下,每次两人可能进行的操作会是什么。
如果第一个人选了正数,第二个人首先会选最小的负数(前提是能选到负数),没有负数第二个人会选 $0$,没有 $0$ 就会选最小的正数。
如果第一个人选了负数,第二个人会选最大的正数,没有正数第二个人会选 $0$,没有 $0$ 会选最小的负数。
如果第一个人选 $0$,第二个人无论怎么选,答案都是 $0$。
那么,我们就可以让第一个人根据第二个人有的数字来确定自己选什么。
分情况讨论,如果第一个人有 $0$,先让答案等于 $0$。
如果第一个人有正数,结合上面的分析,可以得出,答案可能是第一个人的最小正数乘以第二个人的最大负数、第一个人的最大正数乘以第二个人的最小正数、$0$。
负数同理,可能是第一个人的最大负数乘以第二个人的最大正数、第一个人的最小负数乘以第二个人的最大负数、$0$。
那么这个题目就转化为求两个区间的最大正数、最小正数、最大负数、最小负数和是否有 $0$。
最常见的方法是写个线段树,但是由于我线段树太烂~~以及很喜欢分块~~,我最后写了分块。后来我发现,线段树的做法其实比分块要简单太多,我写的分块的码量几乎是别人线段树的两倍。
另外,我发现我打的分块求是否有 $0$ 出了很多奇怪的错误,于是求是否有 $0$ 我使用了前缀和。
以下是带注释的代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN = 100010;
int n, m, q, s, a[MAXN], b[MAXN];
int maxn1a[500], maxn2a[500], minn1a[500], minn2a[500], is0a[MAXN]; // 分块,对应序列 a
int maxn1b[500], maxn2b[500], minn1b[500], minn2b[500], is0b[MAXN]; // 序列 b
struct node {
int maxn1, maxn2, minn1, minn2, is0;
}; // 分别对应最大的正数、最大的负数、最小的正数、最小的负数、是否有 0
node query1(int x, int y) { // 处理序列 a
int ka = x / s, kb = y / s;
node ans;
ans.maxn2 = -0x3f3f3f3f3f3f3f3f;
ans.minn1 = 0x3f3f3f3f3f3f3f3f;
ans.maxn1 = 0;
ans.minn2 = 0;
if(ka == kb) {
for(int i = x; i <= y; i ++) {
if(a[i] < 0) {
ans.maxn2 = max(ans.maxn2, a[i]);
ans.minn2 = min(ans.minn2, a[i]);
}
if(a[i] > 0) {
ans.maxn1 = max(ans.maxn1, a[i]);
ans.minn1 = min(ans.minn1, a[i]);
}
}
return ans;
}
for(int i = x; i < (ka + 1) * s; i ++) {
if(a[i] < 0) {
ans.maxn2 = max(ans.maxn2, a[i]);
ans.minn2 = min(ans.minn2, a[i]);
}
if(a[i] > 0) {
ans.maxn1 = max(ans.maxn1, a[i]);
ans.minn1 = min(ans.minn1, a[i]);
}
}
for(int i = kb * s; i <= y; i ++) {
if(a[i] < 0) {
ans.maxn2 = max(ans.maxn2, a[i]);
ans.minn2 = min(ans.minn2, a[i]);
}
if(a[i] > 0) {
ans.maxn1 = max(ans.maxn1, a[i]);
ans.minn1 = min(ans.minn1, a[i]);
}
}
for(int i = ka + 1; i < kb; i ++) {
ans.maxn2 = max(ans.maxn2, maxn2a[i]);
ans.minn2 = min(ans.minn2, minn2a[i]);
ans.maxn1 = max(ans.maxn1, maxn1a[i]);
ans.minn1 = min(ans.minn1, minn1a[i]);
}
return ans;
}
node query2(int x, int y) { // 序列 b
int ka = x / s, kb = y / s;
node ans;
ans.maxn2 = -0x3f3f3f3f3f3f3f3f;
ans.minn1 = 0x3f3f3f3f3f3f3f3f;
ans.maxn1 = 0;
ans.minn2 = 0;
if(ka == kb) {
for(int i = x; i <= y; i ++) {
if(b[i] < 0) {
ans.maxn2 = max(ans.maxn2, b[i]);
ans.minn2 = min(ans.minn2, b[i]);
}
if(b[i] > 0) {
ans.maxn1 = max(ans.maxn1, b[i]);
ans.minn1 = min(ans.minn1, b[i]);
}
}
return ans;
}
for(int i = x; i < (ka + 1) * s; i ++) {
if(b[i] < 0) {
ans.maxn2 = max(ans.maxn2, b[i]);
ans.minn2 = min(ans.minn2, b[i]);
}
if(b[i] > 0) {
ans.maxn1 = max(ans.maxn1, b[i]);
ans.minn1 = min(ans.minn1, b[i]);
}
}
for(int i = kb * s; i <= y; i ++) {
if(b[i] < 0) {
ans.maxn2 = max(ans.maxn2, b[i]);
ans.minn2 = min(ans.minn2, b[i]);
}
if(b[i] > 0) {
ans.maxn1 = max(ans.maxn1, b[i]);
ans.minn1 = min(ans.minn1, b[i]);
}
}
for(int i = ka + 1; i < kb; i ++) {
ans.maxn2 = max(ans.maxn2, maxn2b[i]);
ans.minn2 = min(ans.minn2, minn2b[i]);
ans.maxn1 = max(ans.maxn1, maxn1b[i]);
ans.minn1 = min(ans.minn1, minn1b[i]);
}
return ans;
}
signed main() {
cin >> n >> m >> q;
s = sqrt(n);
memset(maxn2a, -0x3f, sizeof(maxn2a));
memset(minn1a, 0x3f, sizeof(minn1a));
memset(maxn2b, -0x3f, sizeof(maxn2b));
memset(minn1b, 0x3f, sizeof(minn1b));
for(int i = 1; i <= n; i ++) {
cin >> a[i];
is0a[i] = is0a[i - 1]; // 前缀和处理是否有 0
if(a[i] == 0) {
is0a[i] ++;
}
if(a[i] < 0) {
maxn2a[i / s] = max(maxn2a[i / s], a[i]); // 处理每一块的最大最小值
minn2a[i / s] = min(minn2a[i / s], a[i]);
}
if(a[i] > 0) {
maxn1a[i / s] = max(maxn1a[i / s], a[i]);
minn1a[i / s] = min(minn1a[i / s], a[i]);
}
}
for(int i = 1; i <= m; i ++) {
cin >> b[i];
is0b[i] = is0b[i - 1];
if(b[i] == 0) {
is0b[i] ++;
}
if(b[i] < 0) {
maxn2b[i / s] = max(maxn2b[i / s], b[i]); // 同上
minn2b[i / s] = min(minn2b[i / s], b[i]);
}
if(b[i] > 0) {
maxn1b[i / s] = max(maxn1b[i / s], b[i]);
minn1b[i / s] = min(minn1b[i / s], b[i]);
}
}
for(int i = 1; i <= q; i ++) {
int l1, l2, r1, r2, ans = -0x3f3f3f3f3f3f3f3f;
cin >> l1 >> r1 >> l2 >> r2;
node ans1 = query1(l1, r1);
ans1.is0 = is0a[r1] - is0a[l1 - 1];
node ans2 = query2(l2, r2);
ans2.is0 = is0b[r2] - is0b[l2 - 1]; // 分别求两个区间
if(ans1.is0) {
ans = 0; // 特判序列 a中有 0
}
if(ans1.maxn1) { // 分析中的各种情况分别处理
if(ans2.minn2) {
ans = max(ans, ans1.minn1 * ans2.minn2);
}
else if(ans2.is0) {
ans = max(ans, (int)0);
}
else {
ans = max(ans, ans1.maxn1 * ans2.minn1);
}
}
if(ans1.minn2) {
if(ans2.maxn1) {
ans = max(ans, ans1.maxn2 * ans2.maxn1);
}
else if(ans2.is0) {
ans = max(ans, (int)0);
}
else {
ans = max(ans, ans1.minn2 * ans2.maxn2);
}
}
cout << ans << endl;
}
return 0;
}
题目3782 [CSP 2022S]策略游戏
AAAAAAAAAAAAAAAAAAAA
 11
评论 11
评论
2022-11-06 13:47:26
|
|
|
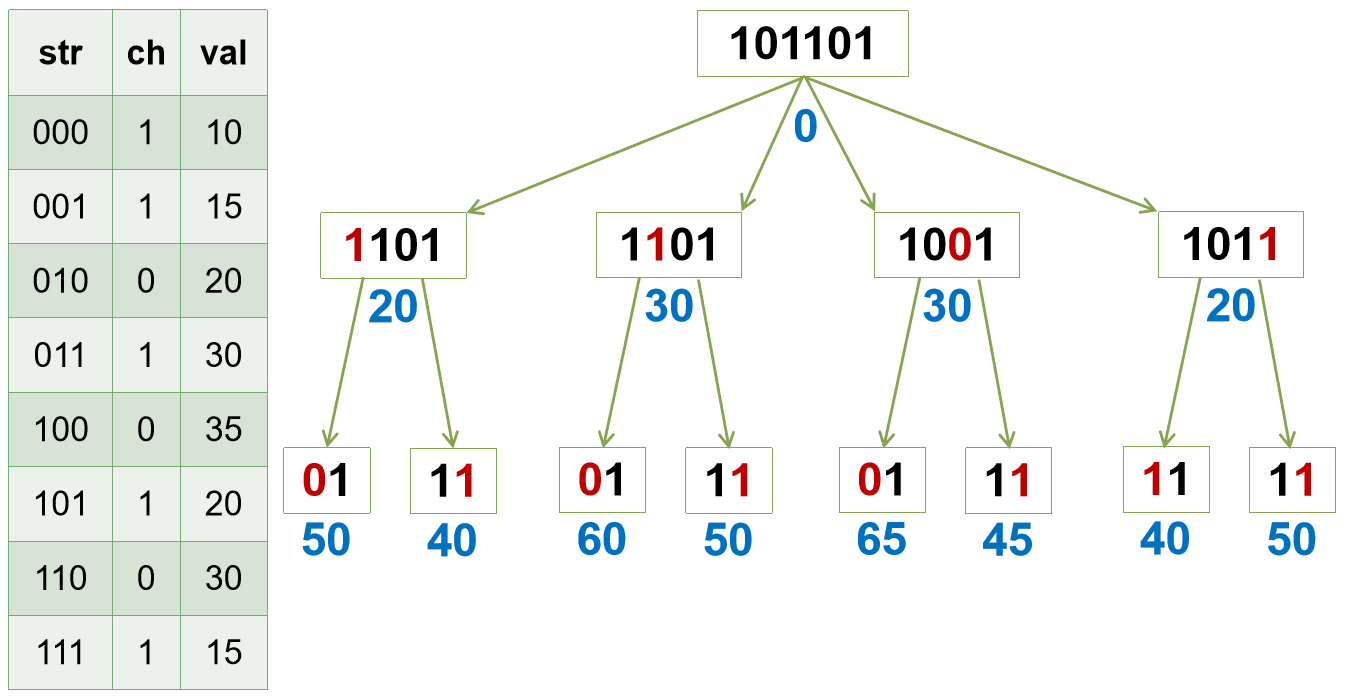
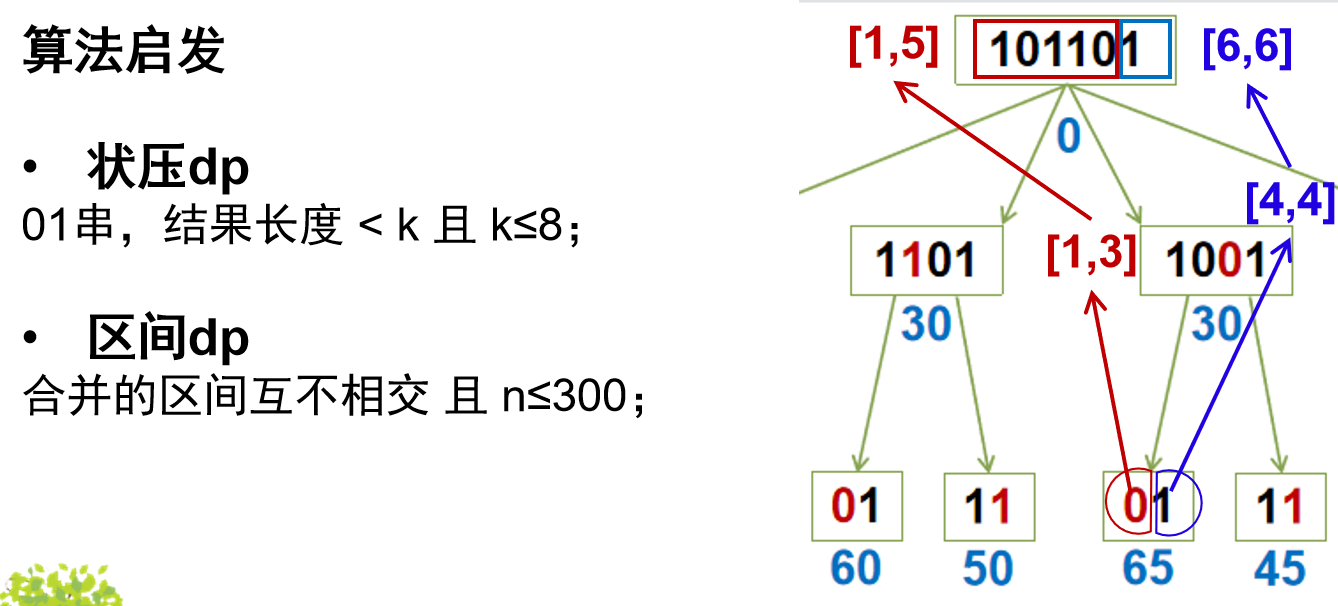
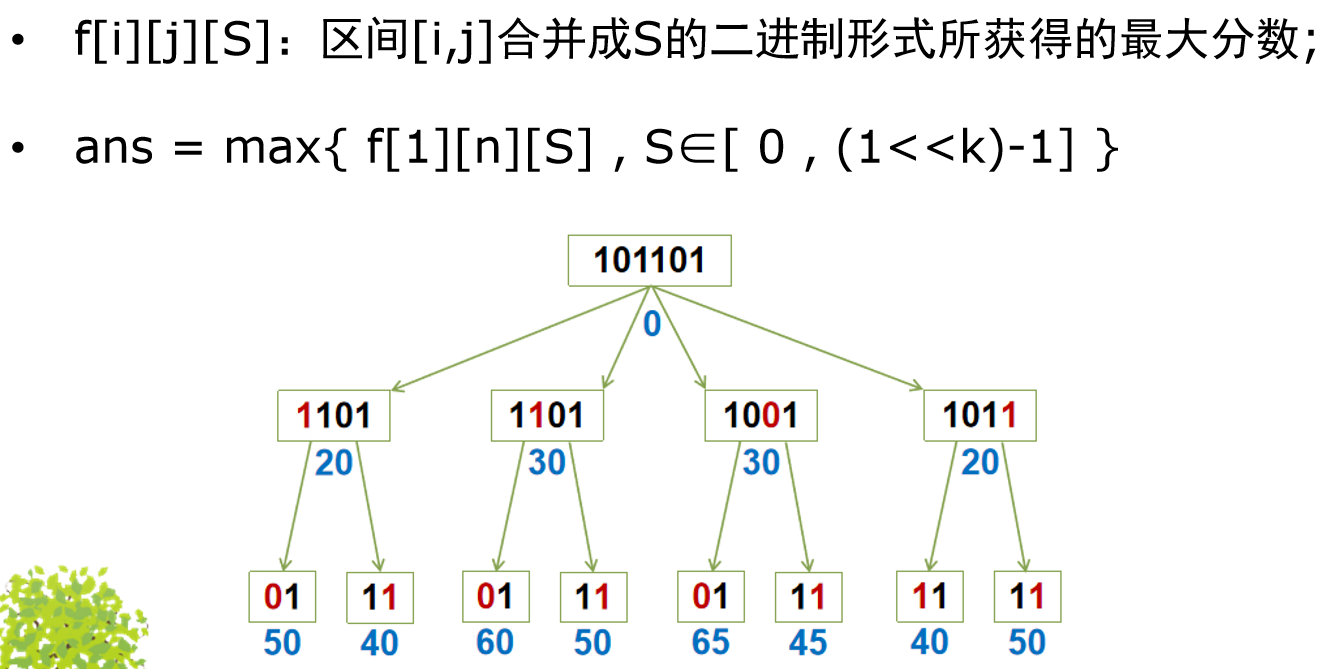
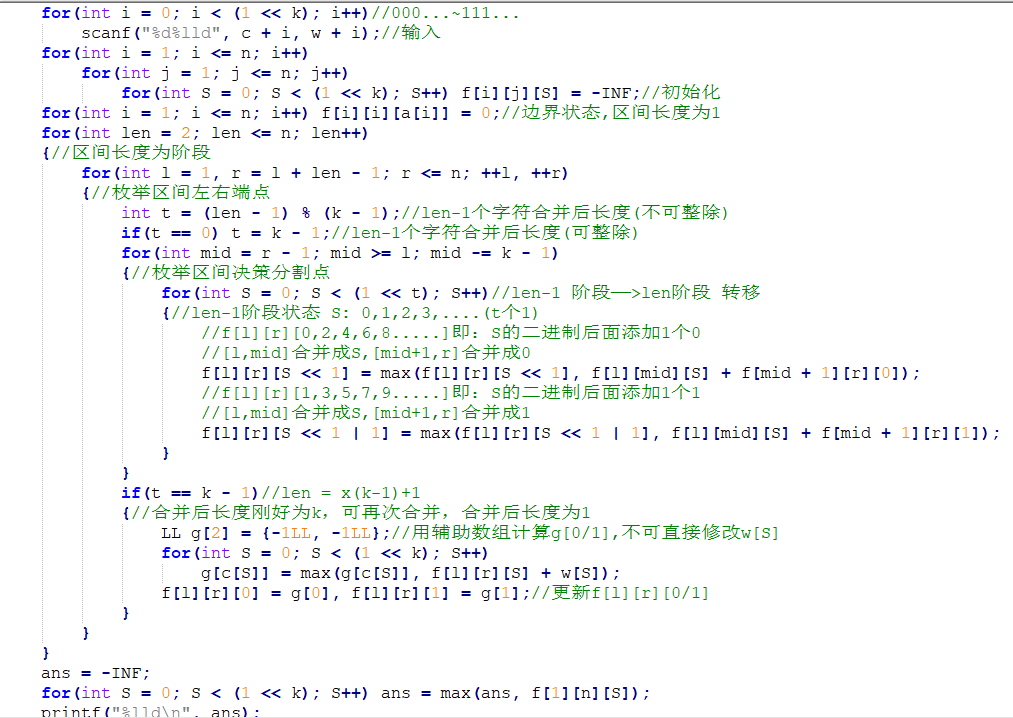
题目2269 [HAOI 2016]字符合并
 7
评论 7
评论
2022-11-05 20:42:23
|
|
|
这题我在考试的时候是100,为什么在这只有40 这题不难,但是容易陷入思维陷阱中。就是说,c++中的<cmath>头文件有直接算出乘方的 pow 函数,但是很明显在这里不能直接用。这里的结果很可能会超过10^18,就会输出乱码。因此我们可以定义一个函数panduan,返回值是long long(结果小于等于10^9),里面是a和b,也是long long.代码如下:
#define ll long long
ll panduan(ll a,ll b){
ll ans=1;
for(ll i=1;i<=b;i++){
ans=ans*a;
if(ans>1000000000) return -1;
}
return ans;
}
然后就可以了,完整代码交给读者自行锻炼
题目3777 [CSP 2022J]乘方
 2
1 条 评论 2
1 条 评论
2022-11-04 11:34:42
|