|
|
Pro3946 信使 题解3946. 信使 题解题目描述给定一个 $n$ 个点 $m$ 条边的有向图,$q$ 次询问从点 $u$ 走 $d$ 步到达点 $v$,且只经过点 $u,v$ 各一次的路径数。答案对 $z$ 取模。 题解原题目要求只经过起点和终点一次的路径数,这个不太好求。但是如果没有这个限制,只要求任意两点之间走 $d$ 步的路径数的话,还是很好求哒! 设 $f[i][j][d]$ 表示:从点 $i$ 走 $d$ 步无限制到达点 $j$ 的路径数。 for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j) if (e[i][j])
f[i][j][1] = 1;
for (int d = 1; d <= 50; ++d)
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
for (int k = 1; k <= n; ++k) if (e[k][j])
f[i][j][d] = (f[i][j][d] + f[i][k][d - 1]);
那么要求从点 $i$ 走 $d$ 步不经过点 $i,j$ 到达点 $j$ 的路径数,就转化为了从点 $i$ 走 $d$ 步无限制到达点 $j$ 的路径数减去从点 $i$ 走 $d$ 步中途经过了点 $i$ 或点 $j$ 到达点 $j$ 的路径数。 简单来说就是,正难则反。合法的方案不好求,就用总方案减去不合法的方案。 设 $h[i][j][d]$ 表示:从点 $i$ 走 $d$ 步不经过点 $i,j$ 到达点 $j$ 的路径数 。想要不合法就在中途的第 $k$ 步($1 \le k \lt d$)走到 $i$ 或 $j$ 即可。
那么从点 $i$ 走 $d$ 步中途经过点 $i$ 或点 $j$ 到达点 $j$ 的路径数 $x$ 即为: $$x = g[i][j][k] * f[i][j][d - k] + h[i][j][k] * f[j][j][d - k]\quad(1 \le k \lt d)$$ 那么 $h[i][j][d] = f[i][j][d] - x$。 接下来考虑如何计算 $g[i][j][d]$(从点 $i$ 走 $d$ 步不经过点 $i,j$ 到达点 $i$ 的路径数)。 同样地,考虑正难则反,求出不合法的路径数,再用总路径数减去不合法的路径数即可。 类似,想要不合法,只需要在中途的第 $k$ 步($1 \le k \lt d$)走到点 $i$ 或点 $j$ 即可。
那么从点 $i$ 走 $d$ 步途中经过点 $i$ 或点 $j$ 到达点 $j$ 的路径数 $y$ 为: $$y = g[i][j][k] * f[i][i][d - k] + h[i][j][k] * f[j][i][d - k] \quad (1 \le k \lt d)$$ 那么 $g[i][j][d] = f[i][j][d] - y$。 这些操作都是在询问之前进行的,每次询问的时候直接输出 $h[u][v][d]$(从点 $u$ 走 $d$ 步不经过点 $u,v$ 到达点 $v$ 的路径数)即可。 代码#include <iostream>
using namespace std;
typedef long long ll;
const int MAXN = 110;
const int MAXD = 60;
ll f[MAXN][MAXN][MAXD]; // f[i][j][d]: tot solution of from i to j with no condition
ll h[MAXN][MAXN][MAXD]; // h[i][j][d]: tot solution of from i to j without passing i or j
ll g[MAXN][MAXN][MAXD]; // g[i][j][d]: tot solution of from i to i without passing i or j
int n, m, q;
int e[MAXN][MAXN];
ll z;
int main() {
freopen("messenger.in", "r", stdin);
freopen("messenger.out", "w", stdout);
cin.tie(0)->sync_with_stdio(false), cout.tie(0);
cin >> n >> m >> z;
for (int i = 1, a, b; i <= m; ++i) {
cin >> a >> b;
e[a][b] = 1;
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (e[i][j]) f[i][j][1] = h[i][j][1] = 1;
}
}
for (int d = 2; d <= 50; ++d) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
for (int k = 1; k <= n; ++k) {
if (e[k][j]) f[i][j][d] = (f[i][j][d] + f[i][k][d - 1]) % z;
}
}
}
}
for (int d = 2; d <= 50; ++d) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (i == j) continue;
// store the illegal paths to h[][][] and g[][][] first
for (int k = 1; k < d; ++k) {
h[i][j][d] = (h[i][j][d] + g[i][j][k] * f[i][j][d - k] + h[i][j][k] * f[j][j][d - k]) % z;
g[i][j][d] = (g[i][j][d] + g[i][j][k] * f[i][i][d - k] + h[i][j][k] * f[j][i][d - k]) % z;
}
h[i][j][d] = (f[i][j][d] - h[i][j][d] + z) % z;
g[i][j][d] = (f[i][i][d] - g[i][j][d] + z) % z;
}
}
}
cin >> q;
for (int u, v, d; q--; ) {
cin >> u >> v >> d;
cout << h[u][v][d] << endl;
}
return 0;
}
题目3946 信使
AAAAAAAAAA
 3
3 条 评论 3
3 条 评论
2025-10-05 14:38:13
|
|
|
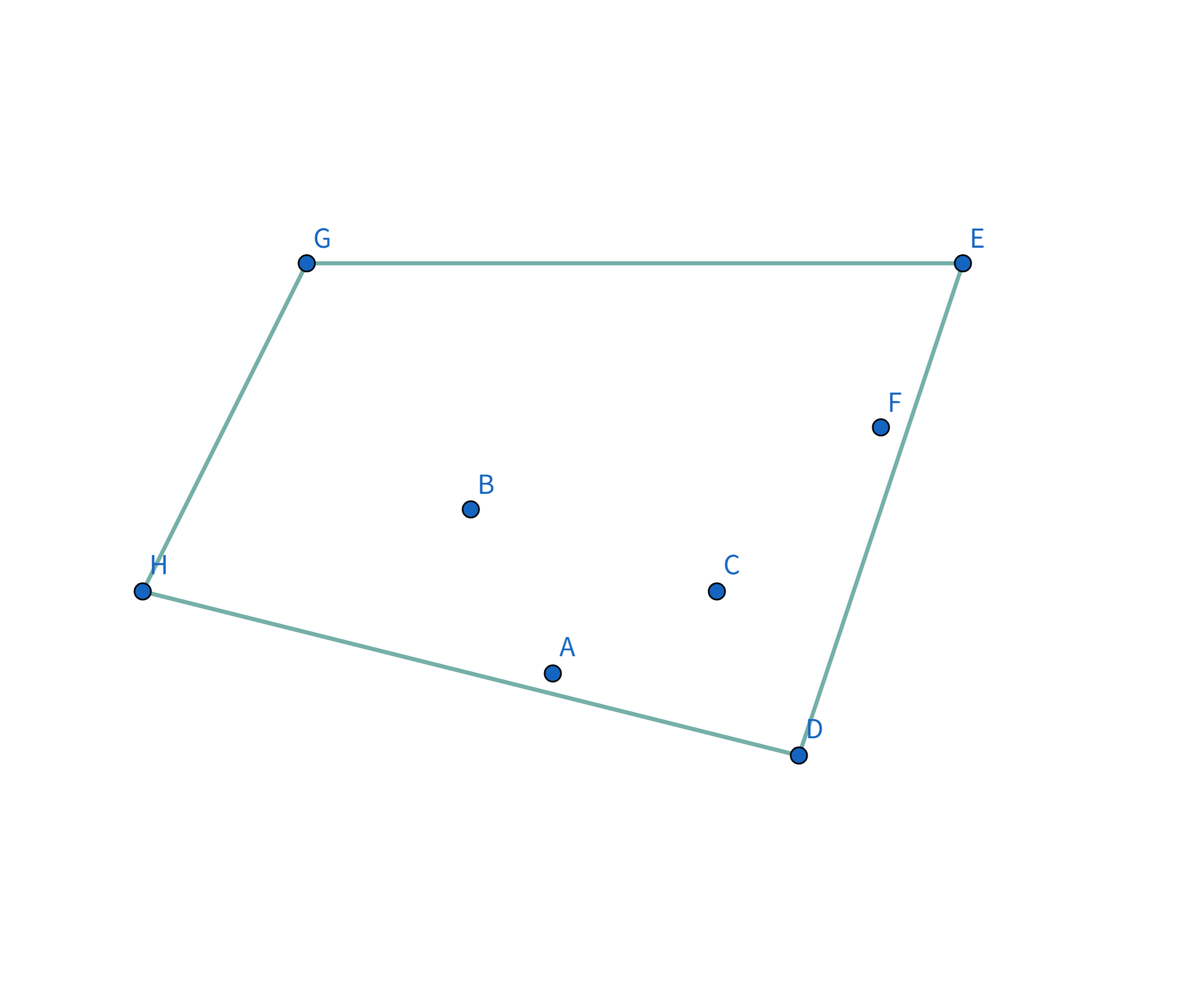
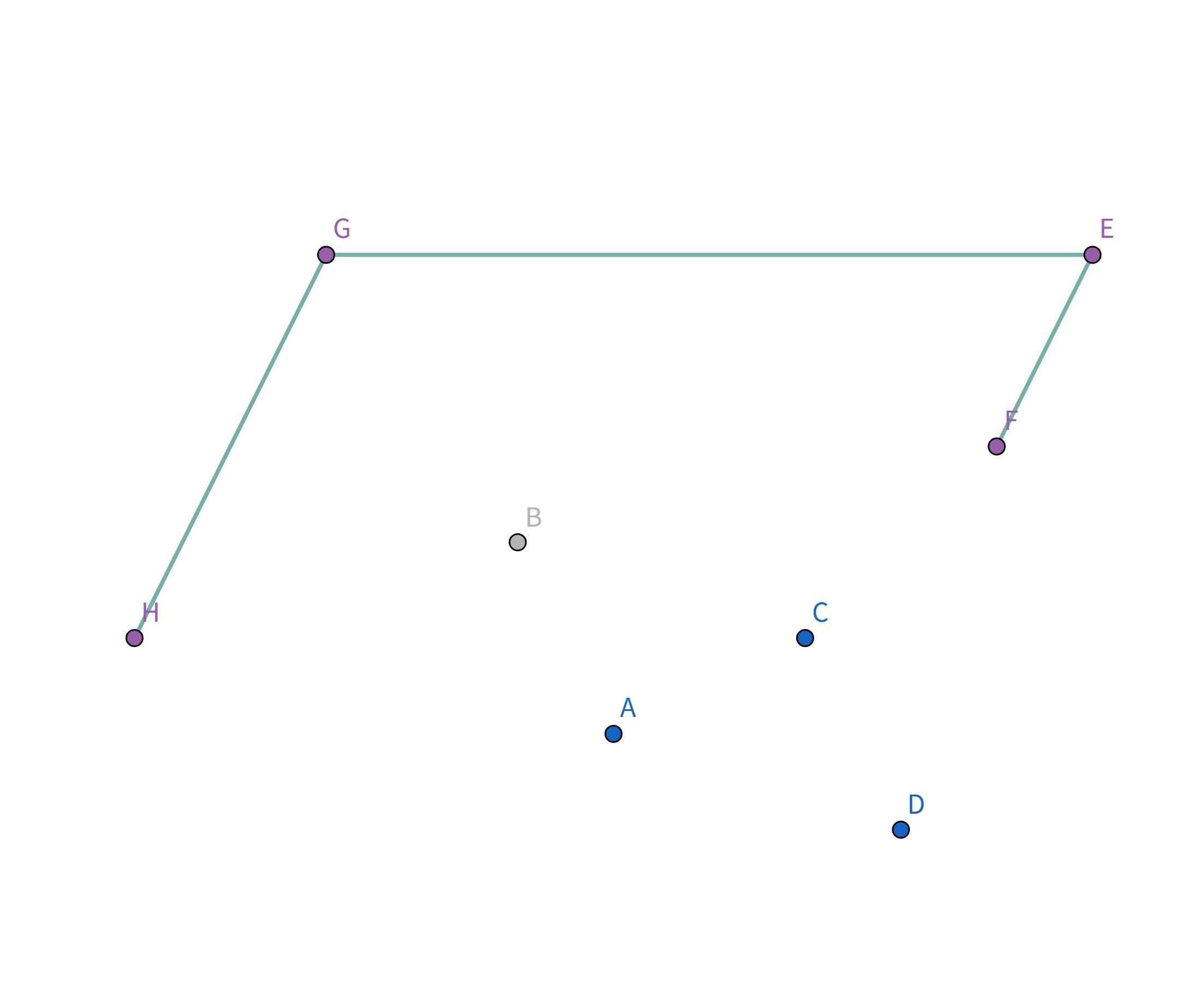
Pro896 圈奶牛 题解896. 圈奶牛 题解题意描述给定有 n 头奶牛,要把这些奶牛用栅栏围起来,栅栏的总长度即为花费,求花费的最小值。 题解例如有这么几头牛:
显然,一个想法是用一个圈把这些牛全部围起来:
但是这样显然不是花费最小的,那我们就让这个椭圆一直缩小,直到和边缘上的点碰触就停止缩小:
这样就是花费最小的啦! 如果再往里缩小的话,花费就会反而变长!
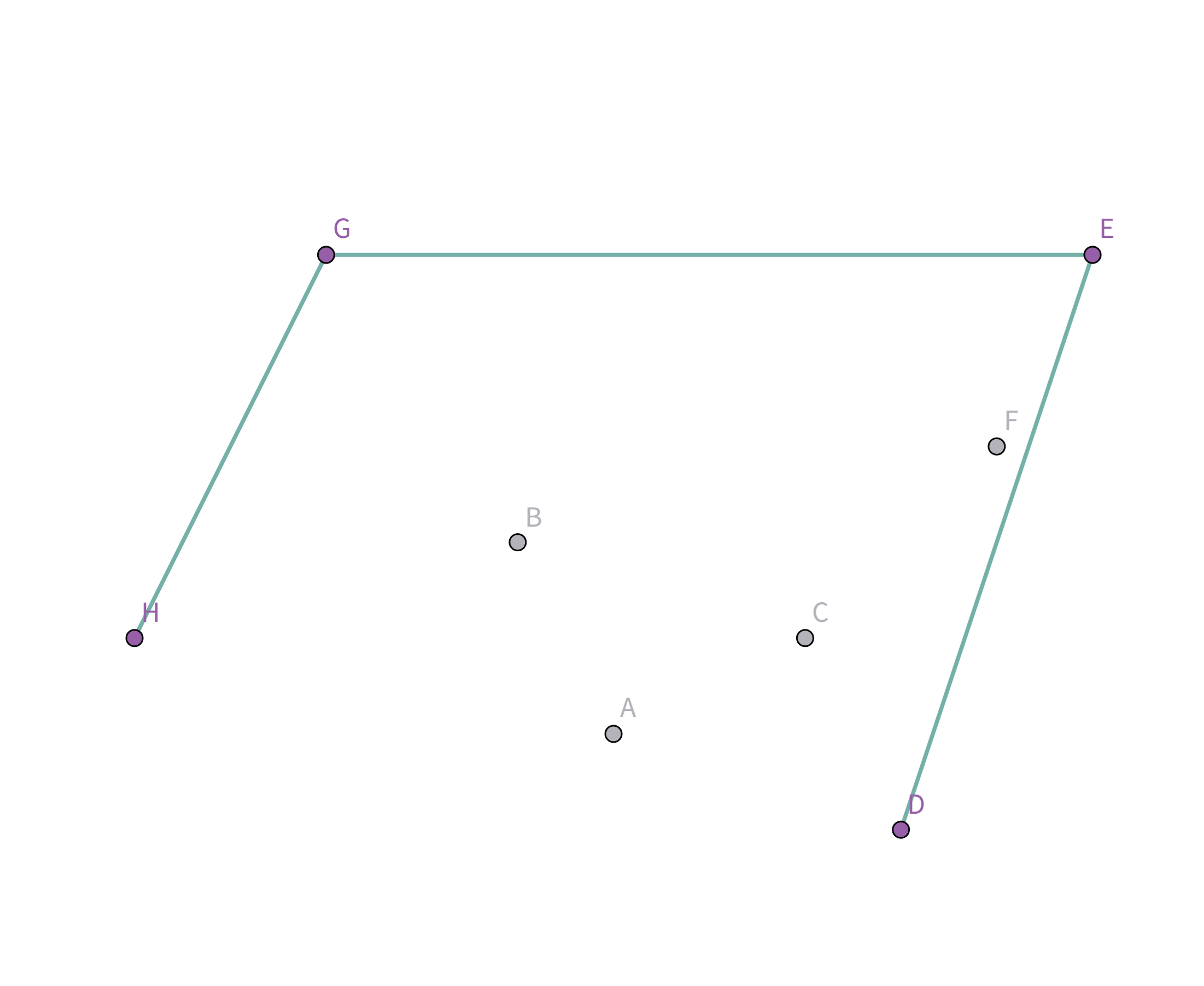
如图,在 $\triangle GHI$ 中,根据三边关系显然有 $GI + IH \gt GH$,所以 $GH$ 就是 $G$ 到 $H$ 花费最小的连接方式。
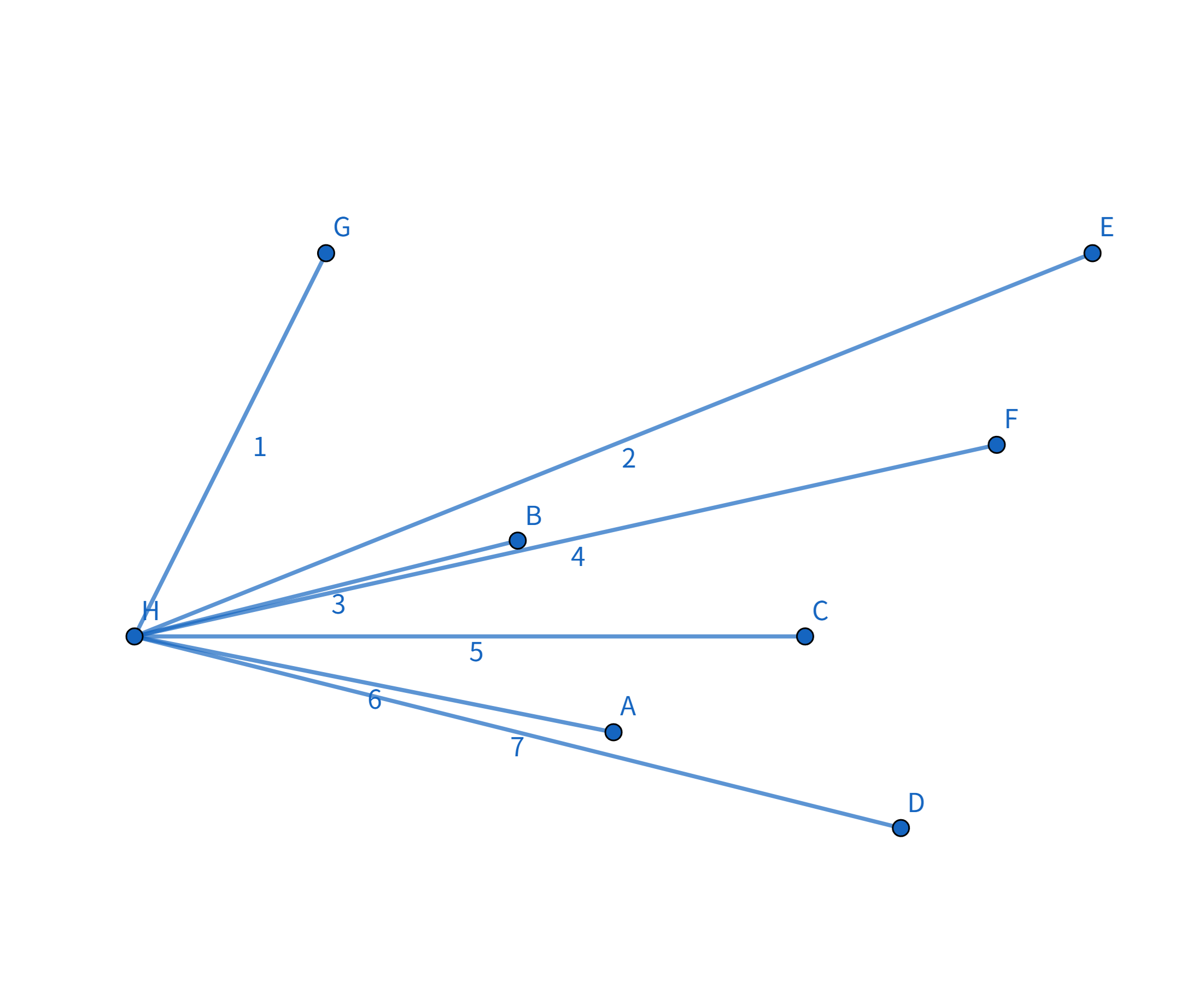
注意到这个连接方式的顶点连线的斜率是递减的 即: $$k_{HG} > k_{GE} > k_{ED} > k_{HD}$$ 那么,我们如何找到这个连接方式呢? 首先找到一个 $x$ 坐标或 $y$ 坐标最大/最小的点,例如图中的点 $H$、点 $G$、点 $E$、点 $D$。 我们以点 $H$ 为例,将这些点排序,按照其他点与点 $H$ 的连线的斜率降序排序(从小到大也可以,只不过实现略有不同):
struct NODE {
double x, y;
} node[MAXN];
double getk(NODE x, NODE y) {
return (x.y - y.y) / (x.x - y.x);
}
int main() {
... // 读入
sort(node + 1, node + n + 1, [](NODE x, NODE y) {
if (x.x != y.x) return x.x < y.x;
return x.y > y.y;
}); // 先进行一个排序,按照 x 坐标为第一关键字升序
// y 坐标为第二关键字降序,也就是要把最左上角的点放到第一个
sort(node + 2, node + n + 1, [](NODE x, NODE y) {
return getk(x, node[1]) > getk(y, node[1]);
});
}
但是 [code](x.x - y.x)[/code] 容易等于零,除数等于零就错误了!那我们就将除法比较改成乘法叭 也就是: $$\frac{a_{1,y} - a_{2,y}}{a_{1,x} - a_{2.x}} \le \frac{b_{1,y} - b_{2,y}}{b_{1,x} - b_{2,x}} \\ \Downarrow \\ (a_{1,y} - a_{2,y})(b_{1,x} - b_{2,x}) \le (b_{1,y} - b_{2,y})(a_{1,x} - a_{2.x})$$
struct NODE {
double x, y;
} node[MAXN];
bool check(NODE a1, NODE a2, NODE b1, NODE b2) {
return (a1.y - a2.y) * (b1.x - b2.x) <= (b1.y - b2.y) * (a1.x - a2.x);
}
double dis(NODE x, NODE y) {
return sqrt(pow(x.x - y.x, 2) + pow(x.y - y.y, 2));
}
int main() {
...
// 找到左上角的点
sort(node + 1, node + n + 1, [](NODE x, NODE y) {
if (x.x != y.x) return x.x < y.x;
return x.y > y.y;
});
// 其余点按照与左上角的点连线的斜率降序排列
sort(node + 2, node + n + 1, [](NODE x, NODE y) {
return !check(x, node[1], y, node[1]);
});
...
}
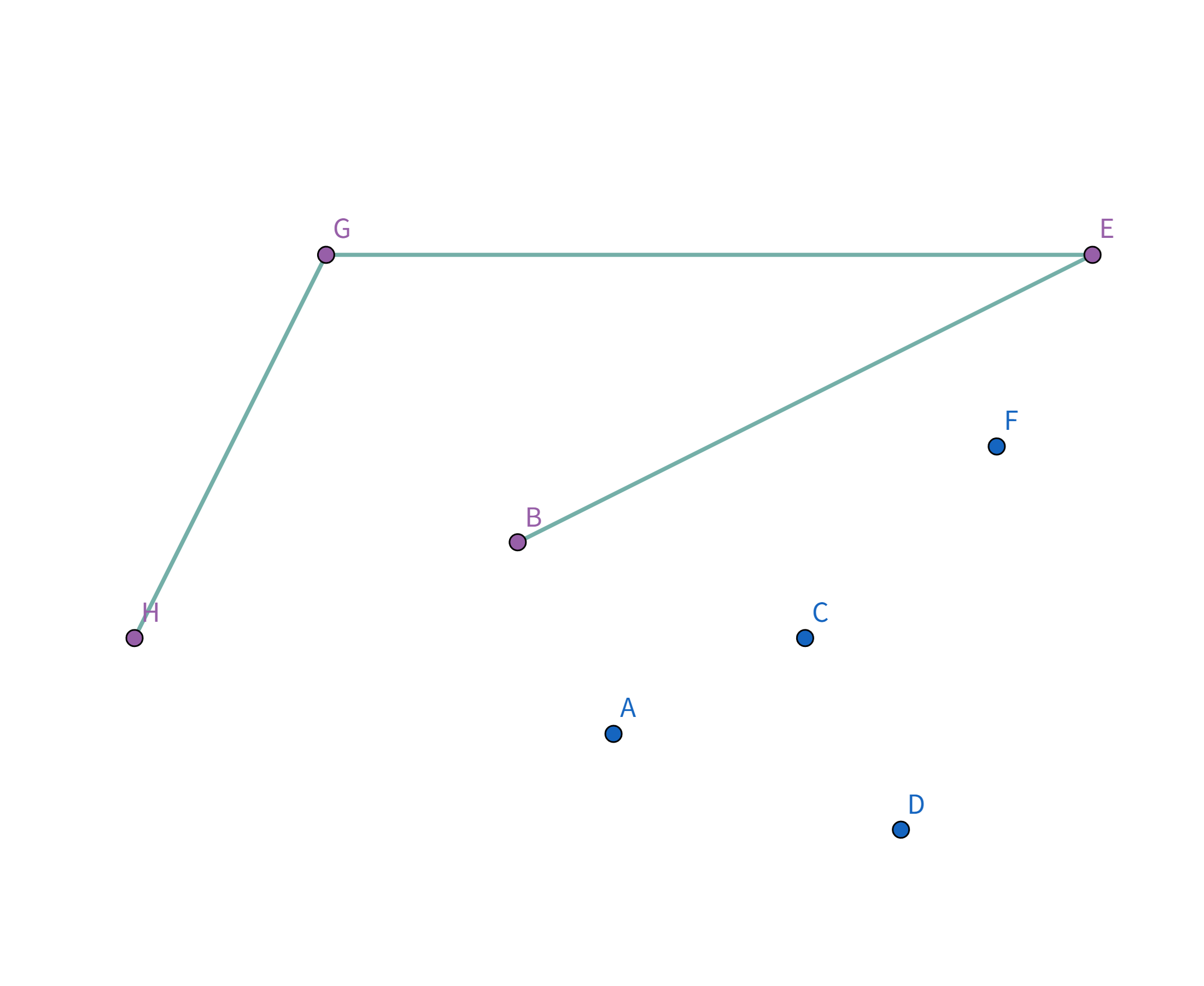
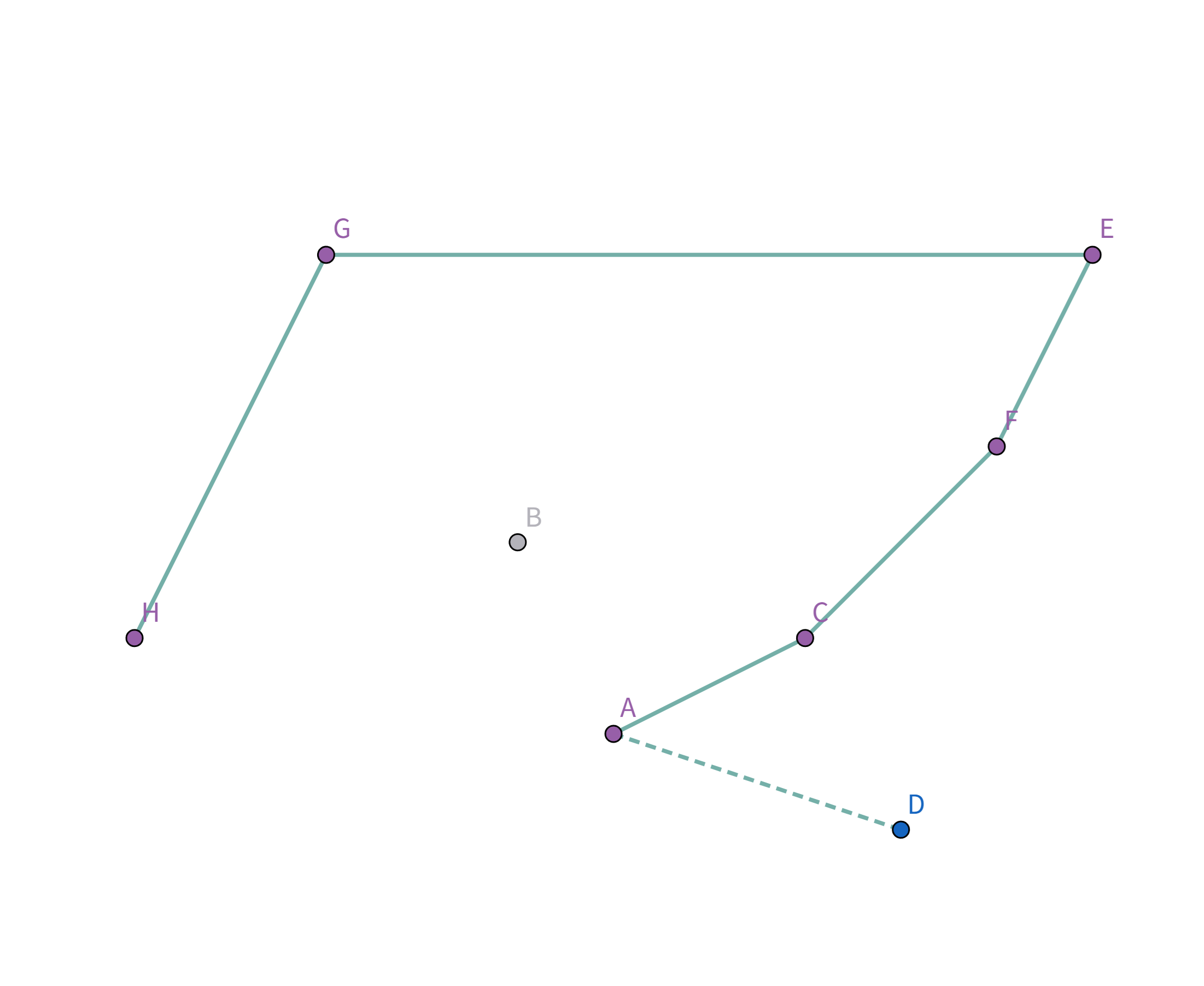
接下来就是考虑怎么样把 $G,H,D,E$ 四个点选中啦! 我们用一个栈来维护选中的点。 首先点集是这样的:
按照排序后的顺序取扫描,首先扫描到点 $H$,此时栈为空,直接把点 $H$ 加入栈:
接着扫描到点 $G$,站内只有一个元素,直接把点 $G$ 加入栈:
接着扫描到点 $E$,发现其与栈顶的点 $G$ 连线的斜率 与之前的所有连线的斜率 满足递减关系,直接入栈:
接着扫描到点 $B$,发现其与栈顶的点 $E$ 连线的斜率 与之前的所有连线的斜率 满足递减关系,直接入栈:
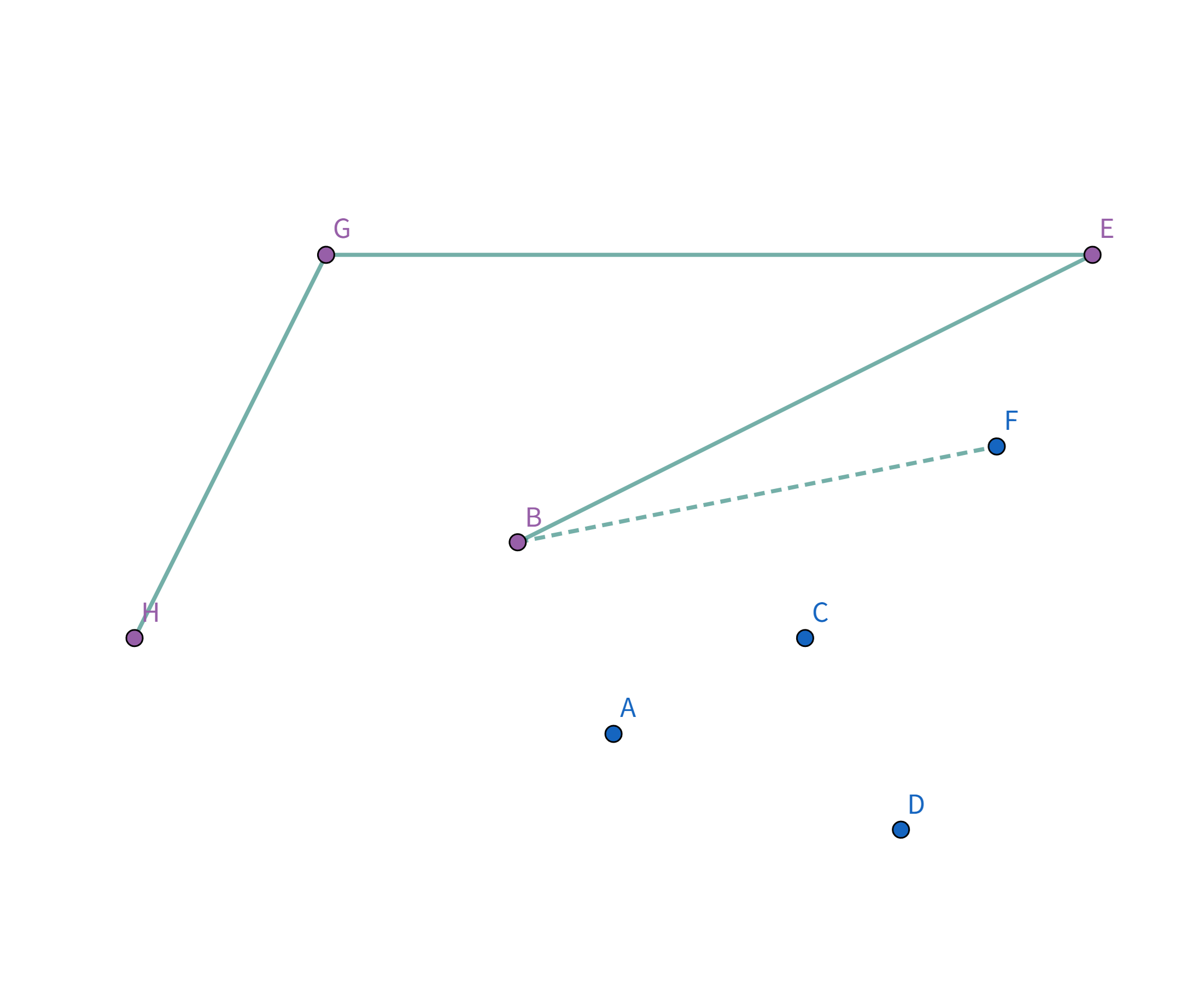
接着扫描到点 $F$!它与栈顶的点 $B$ 的连线斜率比之前大了!
所以把点 $B$ 踢出栈,重复检查点 $F$ 和点 $E$ 的连线是否符合要求。发现其与栈顶的点 $E$ 连线的斜率 与之前的所有连线的斜率 满足递减关系,直接入栈:
接着扫描到点 $C$,发现其与栈顶的点 $F$ 连线的斜率 与之前的所有连线的斜率 满足递减关系,直接入栈:
接着扫描到点 $A$,发现其与栈顶的点 $C$ 连线的斜率 与之前的所有连线的斜率 满足递减关系,直接入栈:
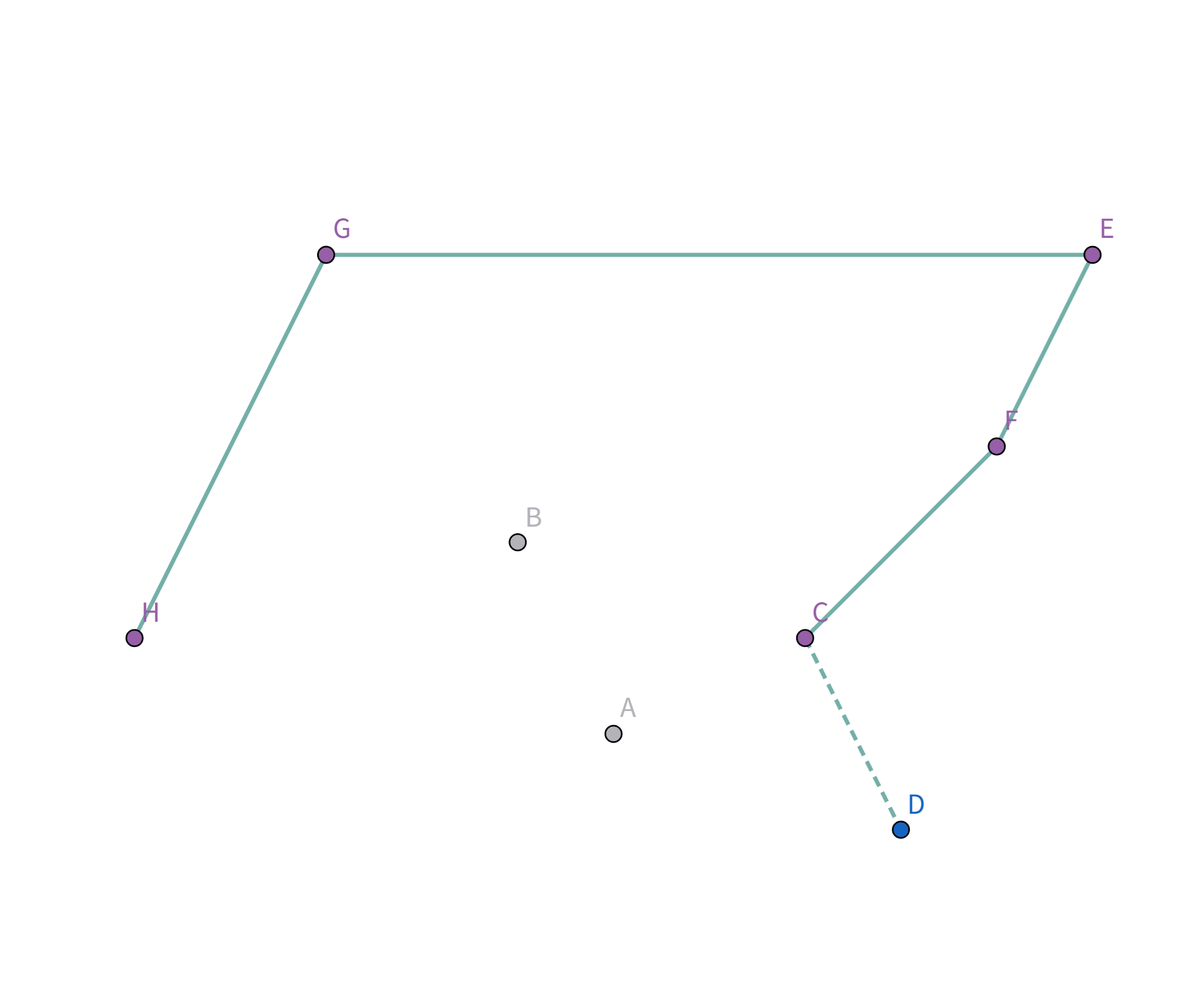
接着扫描到点 $D$!它与栈顶的点 $A$ 连线斜率比之前大!
所以把点 $A$ 踢出栈,重复检查点 $D$ 与栈顶点 $C$ 的连线,发现斜率仍然比之前大!
所以把点 $C$ 踢出栈,重复检查点 $D$ 与栈顶点 $F$ 的连线,发现斜率仍然比之前大!
所以把点 $F$ 踢出栈,重复检查点 $D$ 与栈顶点 $E$ 的连线:
终于满足条件了!点 $D$ 与栈顶点 $E$ 连线的斜率 与之前所有连线的斜率 满足递减关系,所以入栈:
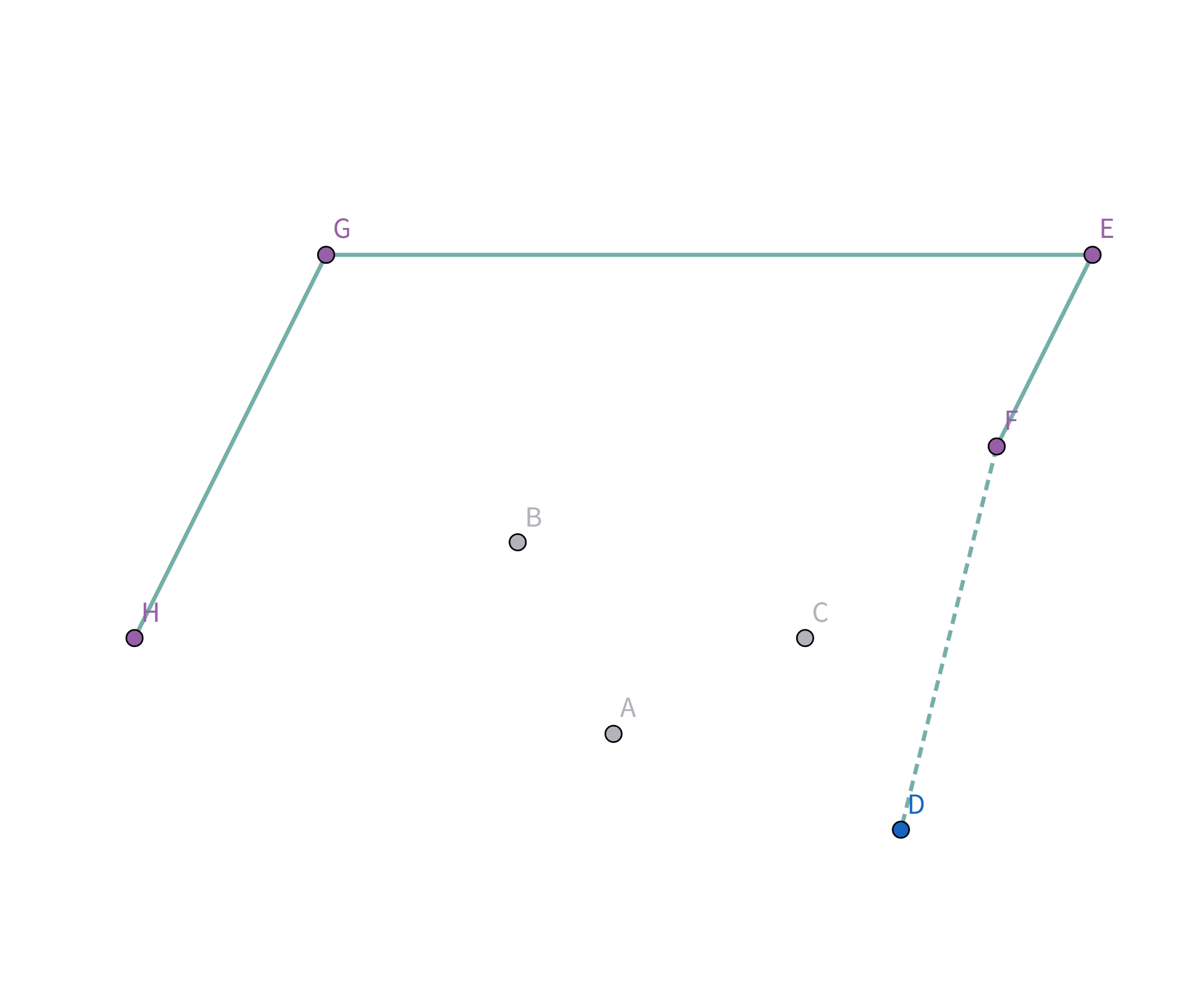
所有的点都扫描完啦!所以把最后的点 $D$ 和第一个点 $H$ 连上就好啦!
和前面的图一模一样哦!这个过程模拟就好啦! (其实判断斜率是否满足要求就看这些线段是不是一直在右转就好嘿嘿) NODE sta[MAXN]; int top;
int main() {
...
sta[++top] = node[1];
for (int i = 2; i <= n; ++i) {
while (top > 1 && !check(node[i], sta[top], sta[top], sta[top - 1])) top--;
sta[++top] = node[i];
}
...
}
此时,栈里面的元素就是要求的点集啦! 最后求花费不是难事: double dis(NODE x, NODE y) {
return sqrt(pow(x.x - y.x, 2) + pow(x.y - y.y, 2));
}
double ans;
int main() {
...
for (int i = 2; i <= top; ++i) {
ans += dis(sta[i], sta[i - 1]);
}
ans += dis(sta[top], sta[1]);
...
}
最终代码:
#include <cstdio>
#include <algorithm>
#include <cmath>
using ::std::sort;
using ::std::pow;
using ::std::sqrt;
const int MAXN = 1e5 + 10;
struct NODE {
double x, y;
} node[MAXN];
bool check(NODE a1, NODE a2, NODE b1, NODE b2) {
return (a1.y - a2.y) * (b1.x - b2.x) <= (b1.y - b2.y) * (a1.x - a2.x);
}
double dis(NODE x, NODE y) {
return sqrt(pow(x.x - y.x, 2) + pow(x.y - y.y, 2));
}
int n;
NODE sta[MAXN];
int top;
double ans;
int main() {
freopen("fc.in", "r", stdin);
freopen("fc.out", "w", stdout);
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%lf %lf", &node[i].x, &node[i].y);
}
sort(node + 1, node + n + 1, [](NODE x, NODE y) {
if (x.x != y.x) return x.x < y.x;
return x.y > y.y;
});
sort(node + 2, node + n + 1, [](NODE x, NODE y) {
return !check(x, node[1], y, node[1]);
});
sta[++top] = node[1];
for (int i = 2; i <= n; ++i) {
while (top > 1 && !check(node[i], sta[top], sta[top], sta[top - 1])) top--;
sta[++top] = node[i];
}
for (int i = 2; i <= top; ++i) {
ans += dis(sta[i], sta[i - 1]);
}
ans += dis(sta[top], sta[1]);
printf("%.2lf\n", ans);
return 0;
}
这个代码交到 COGS 上就能过啦!但是是错误的! HACK输入: 18 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 0 10 0 11 0 12 0 13 0 14 0 15 0 16 0 17 0 18输出: 48.00正确答案: 34.00出现这个问题的原因是所有的点出现在了同一条竖直的线上,数据范围超出了阈值,[code]::std::sort[/code] 函数选择使用快速排序,那么这些点原来按 $y$ 坐标降序的顺序就无法被保证,而这些点传入 [code]check[/code] 函数总是会返回 [code]true[/code],因为 [code]b1.x - b2.x[/code] 和 [code]a1.x - a2.x[/code] 都为 0。最终导致花费计算过多。
解决的办法是排序的时候加上特判。对于在同一条水平的线上的点也用同样的方法就好啦!
sort(node + 2, node + n + 1, [](NODE x, NODE y) {
if (x.x == node[1].x && y.x == node[1].x) return x.y > y.y; // 特判 x 坐标都一样
if (x.y == node[1].y && y.y == node[1].y) return x.x < y.x; // 特判 y 坐标都一样
return !check(x, node[1], y, node[1]);
});
最最终代码:
#include <cstdio>
#include <algorithm>
#include <cmath>
using ::std::sort;
using ::std::pow;
using ::std::sqrt;
const int MAXN = 1e5 + 10;
struct NODE {
double x, y;
} node[MAXN];
bool check(NODE a1, NODE a2, NODE b1, NODE b2) {
return (a1.y - a2.y) * (b1.x - b2.x) <= (b1.y - b2.y) * (a1.x - a2.x);
}
double dis(NODE x, NODE y) {
return sqrt(pow(x.x - y.x, 2) + pow(x.y - y.y, 2));
}
int n;
NODE sta[MAXN];
int top;
double ans;
int main() {
freopen("fc.in", "r", stdin);
freopen("fc.out", "w", stdout);
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%lf %lf", &node[i].x, &node[i].y);
}
sort(node + 1, node + n + 1, [](NODE x, NODE y) {
if (x.x != y.x) return x.x < y.x;
return x.y > y.y;
});
sort(node + 2, node + n + 1, [](NODE x, NODE y) {
if (x.x == node[1].x && y.x == node[1].x) return x.y > y.y;
if (x.y == node[1].y && y.y == node[1].y) return x.x < y.x;
return !check(x, node[1], y, node[1]);
});
sta[++top] = node[1];
for (int i = 2; i <= n; ++i) {
while (top > 1 && !check(node[i], sta[top], sta[top], sta[top - 1])) top--;
sta[++top] = node[i];
}
for (int i = 2; i <= top; ++i) {
ans += dis(sta[i], sta[i - 1]);
}
ans += dis(sta[top], sta[1]);
printf("%.2lf\n", ans);
return 0;
}
时间复杂度:$O(n \log{n} + n)$,瓶颈在排序。
|
|
|
$\newcommand\binom[2]{{#1 \choose #2}}$ 我们先考虑暴力,暴力枚举每一个$i,j$暴力算$\binom{i}{j}$时间复杂度为$O(T*N^3)$,显然超时 然后我们发现$N,M \le2000$我们考虑使用组合数的递推公式预处理$\binom{0}{0}$到$\binom{2000}{2000}$。 这里说一下组合数递推公式$\binom{i}{j}=\binom{i-1}{j-1}+\binom{i-1}{j}$可以从组合意义上来理解 我们从$i$个数中选$j$个数,对于每一个数可以分为选与不选两种情况,选的时候即$\binom{i-1}{j-1}$,在剩下的$i-1$个数里选$j-1$个数,不选的时候即$\binom{i-1}{j}$,在剩下的$i-1$个数里选出$j$个数. 但是这样复杂度为$O(T*N^2+N^2)$,依旧无法通过,事实上我们需要一种不需要枚举$i,j$的方法才能通过。 我们发现对于多个询问,$k$始终为定值,于是考虑前缀和优化,设$ans_{i,j}$,在预处理时,若$k|\binom{i}{j}$,则将$ans_{i,j}+1$。然后套用二维前缀和。但是我们发现,二维前缀和递推时 $ans_{i,j}=ans_{i-1,j}+ans_{i,j-1},-ans_{i-1,j-1}+[k|\binom{i}{j}]$,在处理到边界时,我们会用未处理的值(因为此时$<j$)来更新。但是我们又发现 对于所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 有多少对 $(i,j)$ 满足 $k|\binom{i}{j}$于是我们直接将未处理的值设为同一行上一个值 由此即可AC这道题了!
点我展开看代码#include <bits/stdc++.h>
using namespace std;
#define int long long
int t,n,m,k,c[2008][2008],ans[2008][2008];
void init(){
c[0][0]=1;
c[1][0]=c[1][1]=1;
for(int i=2;i<=2000;i++){
c[i][0]=1;
for(int j=1;j<=i;j++){
c[i][j]=(c[i-1][j-1]+c[i-1][j])%k;
ans[i][j]=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1];
if(c[i][j]==0){
ans[i][j]++;
}
}
ans[i][i+1]=ans[i][i];
}
}
signed main(){
cin>>t>>k;
init();
while(t--){
cin>>n>>m;
if(n<m){
cout<<ans[n][n]<<"\n";
}
else{
cout<<ans[n][m]<<"\n";
}
}
return 0;
}
题目2559 [NOIP 2016]组合数问题
AAAAAAAAAAAAAAAAAAAA
 2
评论 2
评论
2025-10-04 21:32:30
|
|
|
×
提示!该题解未通过审核,建议分享者本着启发他人,照亮自己的初衷以图文并茂形式完善之,请勿粘贴代码。
我们先考虑暴力,暴力枚举每一个$i,j$暴力算$\binom{i}{j}$时间复杂度为$O(T*N^3)$,显然超时 然后我们发现$N,M \le2000$我们考虑使用组合数的递推公式预处理$\binom{0}{0}$到$\binom{2000}{2000}$。 这里说一下组合数递推公式$\binom{i}{j}=\binom{i-1}{j-1}+\binom{i-1}{j}$\可以从组合意义上来理解 我们从$i$个数中选$j$个数,对于每一个数可以分为选与不选两种情况,选的时候即$\binom{i-1}{j-1}$,在剩下的$i-1$个数里选$j-1$个数,不选的时候即$\binom{i-1}{j}$,在剩下的$i-1$个数里选出$j$个数. 但是这样复杂度为$O(T*N^2+N^2)$,依旧无法通过,事实上我们需要一种不需要枚举$i,j$的方法才能通过。
我们发现对于多个询问,$k$始终为定值,于是考虑前缀和优化,设$ans_{i,j}$,在预处理时,若$k|\binom{i}{j}$,则将$an 该题解等待再次审核........................................................................(剩余 2672 个中英字符)
题目2559 [NOIP 2016]组合数问题
AAAAAAAAAAAAAAAAAAAA
2025-09-29 21:59:57
|
|
|
题意 题意:求∑i=1n∑j=1m[i=j](nmodi)⋅(mmodj)。 数据范围:1⩽n,m⩽109。 分析 这是一道简单的推式子题,但是实现比较恶心。 首先不妨设n⩽m(如果n>m交换一下就好了) 然后可以用容斥将题目拆成两个部分: i=1∑nj=1∑m(nmodi)⋅(mmodj)−i=1∑n(nmodi)⋅(mmodi) 将两个求和拆开: i=1∑n(nmodi)⋅j=1∑m(mmodj)−i=1∑n(nmodi)⋅(mmodi) 因为取模很难搞,所以可以用一个性质amodb=a−⌊ba⌋⋅b(取模的定义),将上式转换为: i=1∑n(n−⌊in⌋⋅i)⋅j=1∑m(m−⌊jm⌋⋅j)−i=1∑n(n−⌊in⌋⋅i)⋅(m−⌊im⌋⋅i) 将括号拆开,可以得到: (n2−i=1∑ni⋅⌊in⌋)⋅(m2−i=1∑mi⋅⌊im⌋)−i=1∑n(nm−mi⋅⌊in⌋−ni⋅⌊im⌋+i2⋅⌊in⌋⋅⌊im⌋) 此时我们的复杂度已经是O(n)了,然而这个复杂度仍然不足以通过本题。 要做这道题需要一个简单的技巧——整除分块。 我们很容易发现很多⌊in⌋的值是一样的,且所有的⌊in⌋为一个不下降子序列,呈块状分布 通过简单的计算可以得到,对于每个起点为i的块,它的值为⌊in⌋,终点为⌊⌊in⌋n⌋,然后我们就可以用O(n )的算法计算∑i=1ni⋅⌊in⌋了: 主要步骤,对于每一个块[l,r],它乘号前面前缀和差分得到,即(1+2+⋯+r)−(1+2+⋯+(l−1)),乘号后面的就是⌊ln⌋。 代码: inline long long sum1(long long x){ return x*(x+1)%mod*inv2%mod; } l=1,sum=n*n%mod; while(l<=n){ r=n/(n/l); sum=(sum-(sum1(r)-sum1(l-1)+mod)%mod*(n/l)%mod+mod)%mod; l=r+1; } 同样,∑i=1mi⋅⌊im⌋的值也可以用相同的方法求得。 考虑求∑i=1n(nm−mi⋅⌊in⌋−ni⋅⌊im⌋+i2⋅⌊in⌋⋅⌊im⌋),发现用整除分块完成它需要使区间[l,r]中所有的i都满足⌊in⌋与⌊im⌋相同。 可以用类似的方法,将上面代码中的r=n/(n/l);改为r=min(n/(n/l),m/(m/l));,然后就可以直接求值了! 且慢,虽然前三项nm,mi⋅⌊in⌋,ni⋅⌊im⌋都很容易求得,但是i2⋅⌊in⌋⋅⌊im⌋不是很容易求,因为(12+22+⋯+i2)不好处理。 这里有一个简单的结论:12+22+⋯+n2=6n(n+1)(2n+1),会在文后证明,现在先给出这一部分的代码: inline long long sum2(long long x){ return x*(x+1)%mod*(2*x+1)%mod*inv6%mod; } l=1,tmp3=0; while(l<=n){ long long a,b,c; r=min(n/(n/l),m/(m/l)); a=(r-l+1)*n%mod*m%mod; b=(sum1(r)-sum1(l-1)+mod)%mod*((n/l)*m%mod+(m/l)*n%mod)%mod; c=(sum2(r)-sum2(l-1)+mod)%mod*(n/l)%mod*(m/l)%mod; tmp3=(tmp3+a-b+c+mod)%mod; l=r+1; } 代码 记得开long long取模很恶心,如果错了多半是这种原因因为三个整数相乘会爆long long,因此除法用逆元实现(逆元提前求得) #include<stdio.h> const long long mod=19940417,inv2=9970209,inv6=3323403; long long i,j,k,m,n,l,r,ans,tmp1,tmp2,tmp3; inline long long min(long long a,long long b){ return a<b? a:b; } inline void swp(long long &a,long long &b){ a+=b,b=a-b,a-=b; } inline long long sum1(long long x){ return x*(x+1)%mod*inv2%mod; } inline long long sum2(long long x){ return x*(x+1)%mod*(2*x+1)%mod*inv6%mod; } int main(){ scanf("%lld%lld",&n,&m); if(n>m) swp(n,m); l=1,tmp1=n*n%mod; while(l<=n){ r=n/(n/l); tmp1=(tmp1-(sum1(r)-sum1(l-1)+mod)%mod*(n/l)%mod+mod)%mod; l=r+1; } l=1,tmp2=m*m%mod; while(l<=m){ r=m/(m/l); tmp2=(tmp2-(sum1(r)-sum1(l-1)+mod)%mod*(m/l)%mod+mod)%mod; l=r+1; } l=1,tmp3=0; while(l<=n){ long long a,b,c; r=min(n/(n/l),m/(m/l)); a=(r-l+1)*n%mod*m%mod; b=(sum1(r)-sum1(l-1)+mod)%mod*((n/l)*m%mod+(m/l)*n%mod)%mod; c=(sum2(r)-sum2(l-1)+mod)%mod*(n/l)%mod*(m/l)%mod; tmp3=(tmp3+a-b+c+mod)%mod; l=r+1; } ans=(tmp1*tmp2%mod-tmp3+mod)%mod; printf("%lld\n",ans); return 0; } 简单的证明 证明: 12+22+⋯+n2=6n(n+1)(2n+1) (这个式子可以用简单构造法与数学归纳法证明,由于大部分题解都是用的数学归纳法,且用数学归纳法读者自证不难,因此这里使用简单构造法) 由于有这样一个式子:i2=i2−i+i(i−1)⋅i+i,因此我们可以将这个拆开: 12+22+⋯+n2=i=1∑ni2=i=1∑n(i−1)⋅i+i=1∑ni 然后乘上31: i=1∑ni2=31i=1∑n(i−1)⋅i⋅3+i=1∑ni 构造一下: i=1∑ni2=31i=1∑n(i−1)⋅i⋅((i+1)−(i−2))=31i=1∑n(−(i−2)⋅(i−1)⋅i+(i−1)⋅i⋅(i+1))+i=1∑ni 把它们全部展开: i=1∑ni2=31(−(−1)⋅0⋅1+0⋅1⋅2−0⋅1⋅2+1⋅2⋅3−1⋅2⋅3+⋯(n−1)⋅n⋅(n+1))+2n⋅(n+1) 发现括号里的很多项都可以抵消: i=1∑ni2=3(n−1)⋅n⋅(n+1)+2n⋅(n+1)=6n⋅(n+1)⋅(2(n−1)+3)=6n⋅(n+1)⋅(2n+1) 证毕。 来自洛谷 如有侵权立即删除
题目3668 [清华集训 2012] 模积和
 1
评论 1
评论
2025-09-28 20:59:31
|
|
|
题意 题意:求∑i=1n∑j=1m[i=j](nmodi)⋅(mmodj)。 数据范围:1⩽n,m⩽109。 分析 这是一道简单的推式子题,但是实现比较恶心。 首先不妨设n⩽m(如果n>m交换一下就好了) 然后可以用容斥将题目拆成两个部分: i=1∑nj=1∑m(nmodi)⋅(mmodj)−i=1∑n(nmodi)⋅(mmodi) 将两个求和拆开: i=1∑n(nmodi)⋅j=1∑m(mmodj)−i=1∑n(nmodi)⋅(mmodi) 因为取模很难搞,所以可以用一个性质amodb=a−⌊ba⌋⋅b(取模的定义),将上式转换为: i=1∑n(n−⌊in⌋⋅i)⋅j=1∑m(m−⌊jm⌋⋅j)−i=1∑n(n−⌊in⌋⋅i)⋅(m−⌊im⌋⋅i) 将括号拆开,可以得到: (n2−i=1∑ni⋅⌊in⌋)⋅(m2−i=1∑mi⋅⌊im⌋)−i=1∑n(nm−mi⋅⌊in⌋−ni⋅⌊im⌋+i2⋅⌊in⌋⋅⌊im⌋) 此时我们的复杂度已经是O(n)了,然而这个复杂度仍然不足以通过本题。 要做这道题需要一个简单的技巧——整除分块。 我们很容易发现很多⌊in⌋的值是一样的,且所有的⌊in⌋为一个不下降子序列,呈块状分布 通过简单的计算可以得到,对于每个起点为i的块,它的值为⌊in⌋,终点为⌊⌊in⌋n⌋,然后我们就可以用O(n )的算法计算∑i=1ni⋅⌊in⌋了: 主要步骤,对于每一个块[l,r],它乘号前面前缀和差分得到,即(1+2+⋯+r)−(1+2+⋯+(l−1)),乘号后面的就是⌊ln⌋。 代码: inline long long sum1(long long x){ return x*(x+1)%mod*inv2%mod; } l=1,sum=n*n%mod; while(l<=n){ r=n/(n/l); sum=(sum-(sum1(r)-sum1(l-1)+mod)%mod*(n/l)%mod+mod)%mod; l=r+1; } 同样,∑i=1mi⋅⌊im⌋的值也可以用相同的方法求得。 考虑求∑i=1n(nm−mi⋅⌊in⌋−ni⋅⌊im⌋+i2⋅⌊in⌋⋅⌊im⌋),发现用整除分块完成它需要使区间[l,r]中所有的i都满足⌊in⌋与⌊im⌋相同。 可以用类似的方法,将上面代码中的r=n/(n/l);改为r=min(n/(n/l),m/(m/l));,然后就可以直接求值了! 且慢,虽然前三项nm,mi⋅⌊in⌋,ni⋅⌊im⌋都很容易求得,但是i2⋅⌊in⌋⋅⌊im⌋不是很容易求,因为(12+22+⋯+i2)不好处理。 这里有一个简单的结论:12+22+⋯+n2=6n(n+1)(2n+1),会在文后证明,现在先给出这一部分的代码: inline long long sum2(long long x){ return x*(x+1)%mod*(2*x+1)%mod*inv6%mod; } l=1,tmp3=0; while(l<=n){ long long a,b,c; r=min(n/(n/l),m/(m/l)); a=(r-l+1)*n%mod*m%mod; b=(sum1(r)-sum1(l-1)+mod)%mod*((n/l)*m%mod+(m/l)*n%mod)%mod; c=(sum2(r)-sum2(l-1)+mod)%mod*(n/l)%mod*(m/l)%mod; tmp3=(tmp3+a-b+c+mod)%mod; l=r+1; } 代码 记得开long long取模很恶心,如果错了多半是这种原因因为三个整数相乘会爆long long,因此除法用逆元实现(逆元提前求得) #include<stdio.h> const long long mod=19940417,inv2=9970209,inv6=3323403; long long i,j,k,m,n,l,r,ans,tmp1,tmp2,tmp3; inline long long min(long long a,long long b){ return a<b? a:b; } inline void swp(long long &a,long long &b){ a+=b,b=a-b,a-=b; } inline long long sum1(long long x){ return x*(x+1)%mod*inv2%mod; } inline long long sum2(long long x){ return x*(x+1)%mod*(2*x+1)%mod*inv6%mod; } int main(){ scanf("%lld%lld",&n,&m); if(n>m) swp(n,m); l=1,tmp1=n*n%mod; while(l<=n){ r=n/(n/l); tmp1=(tmp1-(sum1(r)-sum1(l-1)+mod)%mod*(n/l)%mod+mod)%mod; l=r+1; } l=1,tmp2=m*m%mod; while(l<=m){ r=m/(m/l); tmp2=(tmp2-(sum1(r)-sum1(l-1)+mod)%mod*(m/l)%mod+mod)%mod; l=r+1; } l=1,tmp3=0; while(l<=n){ long long a,b,c; r=min(n/(n/l),m/(m/l)); a=(r-l+1)*n%mod*m%mod; b=(sum1(r)-sum1(l-1)+mod)%mod*((n/l)*m%mod+(m/l)*n%mod)%mod; c=(sum2(r)-sum2(l-1)+mod)%mod*(n/l)%mod*(m/l)%mod; tmp3=(tmp3+a-b+c+mod)%mod; l=r+1; } ans=(tmp1*tmp2%mod-tmp3+mod)%mod; printf("%lld\n",ans); return 0; } 简单的证明 证明: 12+22+⋯+n2=6n(n+1)(2n+1) (这个式子可以用简单构造法与数学归纳法证明,由于大部分题解都是用的数学归纳法,且用数学归纳法读者自证不难,因此这里使用简单构造法) 由于有这样一个式子:i2=i2−i+i(i−1)⋅i+i,因此我们可以将这个拆开: 12+22+⋯+n2=i=1∑ni2=i=1∑n(i−1)⋅i+i=1∑ni 然后乘上31: i=1∑ni2=31i=1∑n(i−1)⋅i⋅3+i=1∑ni 构造一下: i=1∑ni2=31i=1∑n(i−1)⋅i⋅((i+1)−(i−2))=31i=1∑n(−(i−2)⋅(i−1)⋅i+(i−1)⋅i⋅(i+1))+i=1∑ni 把它们全部展开: i=1∑ni2=31(−(−1)⋅0⋅1+0⋅1⋅2−0⋅1⋅2+1⋅2⋅3−1⋅2⋅3+⋯(n−1)⋅n⋅(n+1))+2n⋅(n+1) 发现括号里的很多项都可以抵消: i=1∑ni2=3(n−1)⋅n⋅(n+1)+2n⋅(n+1)=6n⋅(n+1)⋅(2(n−1)+3)=6n⋅(n+1)⋅(2n+1) 证毕。
题目3668 [清华集训 2012] 模积和
AAAAAAAAAA
 1
评论 1
评论
2025-09-28 20:51:34
|