更好的阅读体验：https://www.cnblogs.com/To-Carpe-Diem/p/19555785

大意

求 $[l, r]$ 内有多少数，满足 $本身 \mod 数位和 = 0$ ，则记一次贡献。

........................................................................

该题解待审

更好的阅读体验：https://www.cnblogs.com/To-Carpe-Diem/p/19555727

大意

求一段区间 $[l, r]$ 里面的 $(i, j)$ 二元组，满足 $s[i] \oplus s[i + 1] \cdots \oplus s[j] = k$。

思路

首先，我们不难想到这个异或的性质可以扩展，然后，我们可以考虑用莫队求解此题。

对于询问分块，那我们只需要考虑加入一个点与删除一个点对 $ans$ 的

........................................................................

该题解待审

看到这个题的第一眼就气笑了，都 2026 年了，出题人企图让我在代码里用小数运算。

这给了我一个提示：说不定这个与众不同题其实就是要用一些与众不同的算法。

注意到分配最多摊位的社团与分配最少摊位的社团的摊位差不超过 $30$，因为对于任意 $i,j$，都有 $u_i\times 2^{30}>u_j$。

好的，我们先执行这样的操作若干轮：每次都给

........................................................................

该题解待审

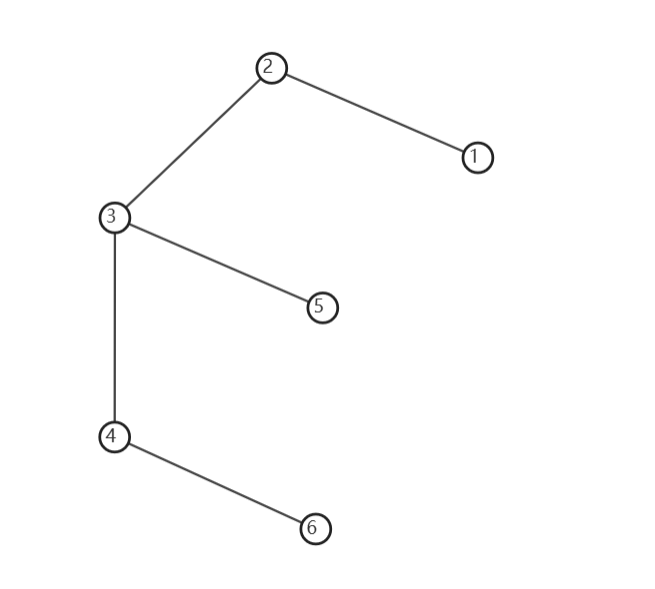
喜提最劣解（常数最大解）。第一遍甚至读错题一个小时，喜提视力最好奖。

不难发现题目要求除了给定的黑点外其他点不能染成黑色（就是读错在这里了）。

因此不难发现，若一个灰点周围有至少一个黑点，则这个点要满足两个条件之一。

一：这个点初始染成白色

二：这个点与一个初始染成白色的点相连。

然后就是很基础的东西了，因为相连在树上有儿子和父亲的关系，所以要分讨几种情况。

假如说将 $1,5,6$ 染成黑色，答案为 $1$，将 $3$ 染成白色即可，可以手玩一下，就知道怎么设置状态了。

设 $dp_{x,0/1/

........................................................................

该题解待审

感觉像是什么很复杂的博弈，应该是结论题，但是我不会猜结论。

考虑一些简单的做法，先特判掉 $n\le 3$ 的情况，因为此时一步能到达所有格子。

其他情况考虑二分答案 $mid$，判断能否得到 $\ge mid$ 的分数，这样令 $b_i=[a_i<mid]$，我们将问题转化为能否取到 $0$。

若 $b_i$ 的 $1$ 的个数

........................................................................

该题解待审

讲个笑话：交当年自己写的题解的代码，结果忘了自己当年习惯在题解代码里加反作弊了。

在此之前，我们要先知道异或运算是个什么东西：就是将两个二进制数的最低位对其，依次比较两个二进制数的每一位，如果相同，则得到的结果为 $0$，不同则为 $1$。

从定义可以推导出来的结论：对于任意 $x$，都有 $x\oplus x=0$，应为两个相同的数二进制上每一位都相同，所以结果一定为 $0$，同理可以推出 $x\oplus 0=x$。这里不多做叙述。（$\oplus$ 为异或的运算符号）

我们定义 $s_i=a_1\oplus a_2\oplus\dots\oplus a_i $。显然 $a_l\oplus a_{l+1}\oplus\dots\oplus a_r=s_r\oplus s_{l-1}$。基于的原理便是 $x\oplus x=0$。应为 $s_r,s_{l-1}$ 都包含 $s_{l-1}$ 这个部分，所以相抵消，只剩下 $[l,r]$ 这部分的异或和。

根据异或的定义，我们可以很方便的推出：如果 $a\oplus b=k$，那么 $a\oplus k=b,b\oplus k=a$。

结论部分讲解完毕，让我们回到题面，注意到是区间静态问题，不要求强制在线，显然可以用莫队乱搞。

我们在上文提到 $s_r\oplus s_{l-1}$ 即为 $[l,r]$ 区间的异或和。可以将问题转化为：每次给出区间 $[L,R]$，求出 $\sum\limits_{L-1\le i,j\le R}[s_i\oplus s_j=k]$。我们可以开一个桶 $cnt$，$cnt_{s_i}$ 为当前区间中，$s_i$ 的个数。当前区间异或和为 $k$ 的子区间数量为 $ans$。

如果有 $s_i\oplus s_j=k$，那么必然 $s_i\oplus k=s_j$。如果当前区间左右边界移动时，区间内多了一个 $s_i$，那么该区间内所有的 $s_j$ 与其的异或和是 $k$，区间内 $s_j$ 的数量为 $cnt_{s_j}$，所以对当前区间答案的贡献为 $cnt_{s_j}$。在将 $cnt_{s_i}+1$。我们就完成了区间的扩张。

已知 $s_i,k$，如何快速找到 $s_j$ 使得 $s_i\oplus s_j=k$。根据异或运算的性质 $s_j=s_i\oplus k$。

坑点大全：

1. 因为询问是区间 $[L,R]$，而处理时会将 $L-1$。所以会出现左边界为 $0$ 的情况。因此莫队中两个指针的初始位置都是 $0$.

2. 初始情况下，区间包含 $s_0=0$，所以 $cnt_0$ 初值为 $1$。

3. 当 $k=0$ 时，对于任何 $a$ 都有 $a\oplus 0=a$。因此在删除时，应当先对 $cnt$ 操作，再对答案 $ans$ 操作（我 WA 了好几次）。

4. 虽然 $a_i$ 小于 $10^5$，但如果 $a_1=100000,a_2=31071$，$s_2$ 有最大值为 $ 131071$。所以 $cnt$ 的大小一定要把控好（好像数据不卡这个）。