|
当 $k$ 较大时
-
黑色格无三连……
-
任意三个连续的格子中至多有两个黑色格……
-
黑色格比例 $\le \frac{2}{3}$
-
$k > \left\lfloor\frac{2}{3}n\right\rfloor$ 时无解。
构造答案
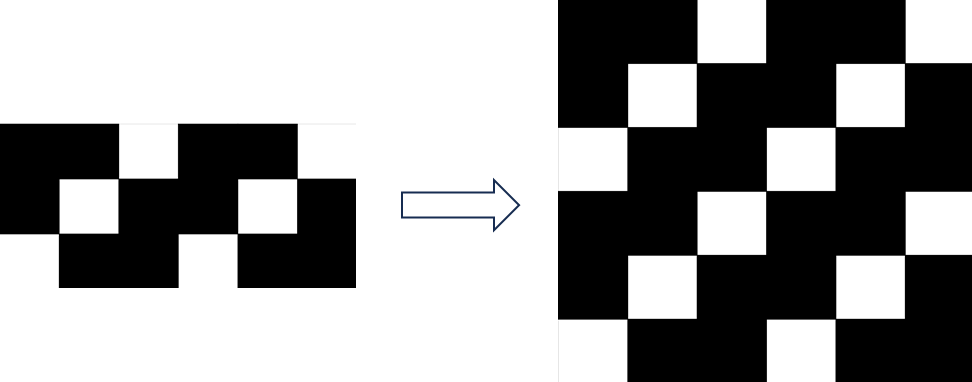
$k = \frac{2}{3}n$
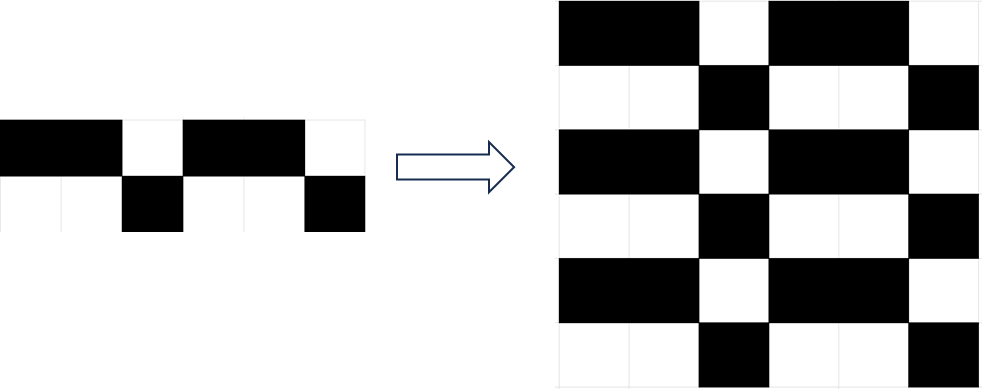
$k = \frac{1}{2}n$
可见,它们可自由组合
$\left\lceil\frac{1}{2}n\right\rceil \le n \le \left\lfloor\frac{2}{3}n\right\rfloor$ 时均可构造。
目前的结论
-
$k > \left\lfloor\frac{2}{3}n\right\rfloor$ 时无解。
-
$\left\lceil\frac{1}{2}n\right\rceil \le n \le \left\lfloor\frac{2}{3}n\right\rfloor$ 时可通过组合基本型来构造合法答案;
-
$k < \left\lceil\frac{1}{2}n\right\rceil$ 时……无解
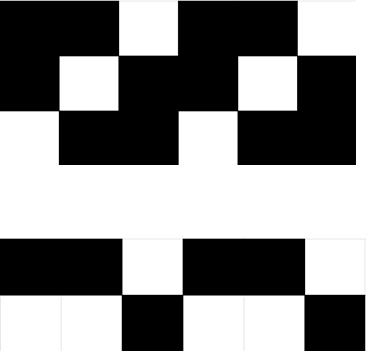
$k < \left\lceil\frac{1}{2}n\right\rceil$ 时一定有白色格三连?
-
显然 $n$ 越大,$k$ 越小时越容易产生白色格三连,因此不妨默认 $n$ 为奇数且 $k=\left\lceil\frac{1}{2}n\right\rceil - 1$。
-
先从最基本的 $n=5, k=2$ 开始...
$n=5, k=2$
-
以下称第 $j$ 列从上至下第 $i$ 个黑色格为“第 $i$ 条链的第 $j$ 个格子”;
-
第 2 条链的格子分布?
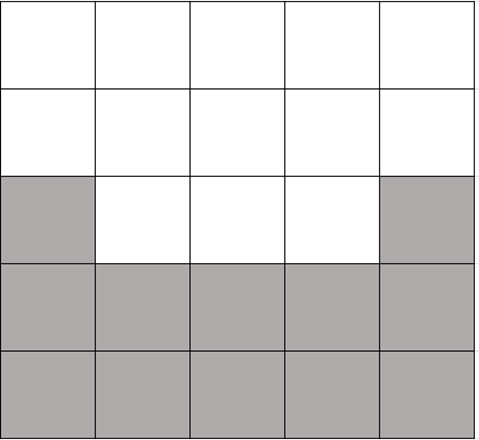
第 1, 5 列的范围是显然的;
如果第 2 条链的第 2/3/4 个格子在第 3 行的话...
-
第 2 条链的格子分布;
-
由对称性得到第 1 条链的分布;
-
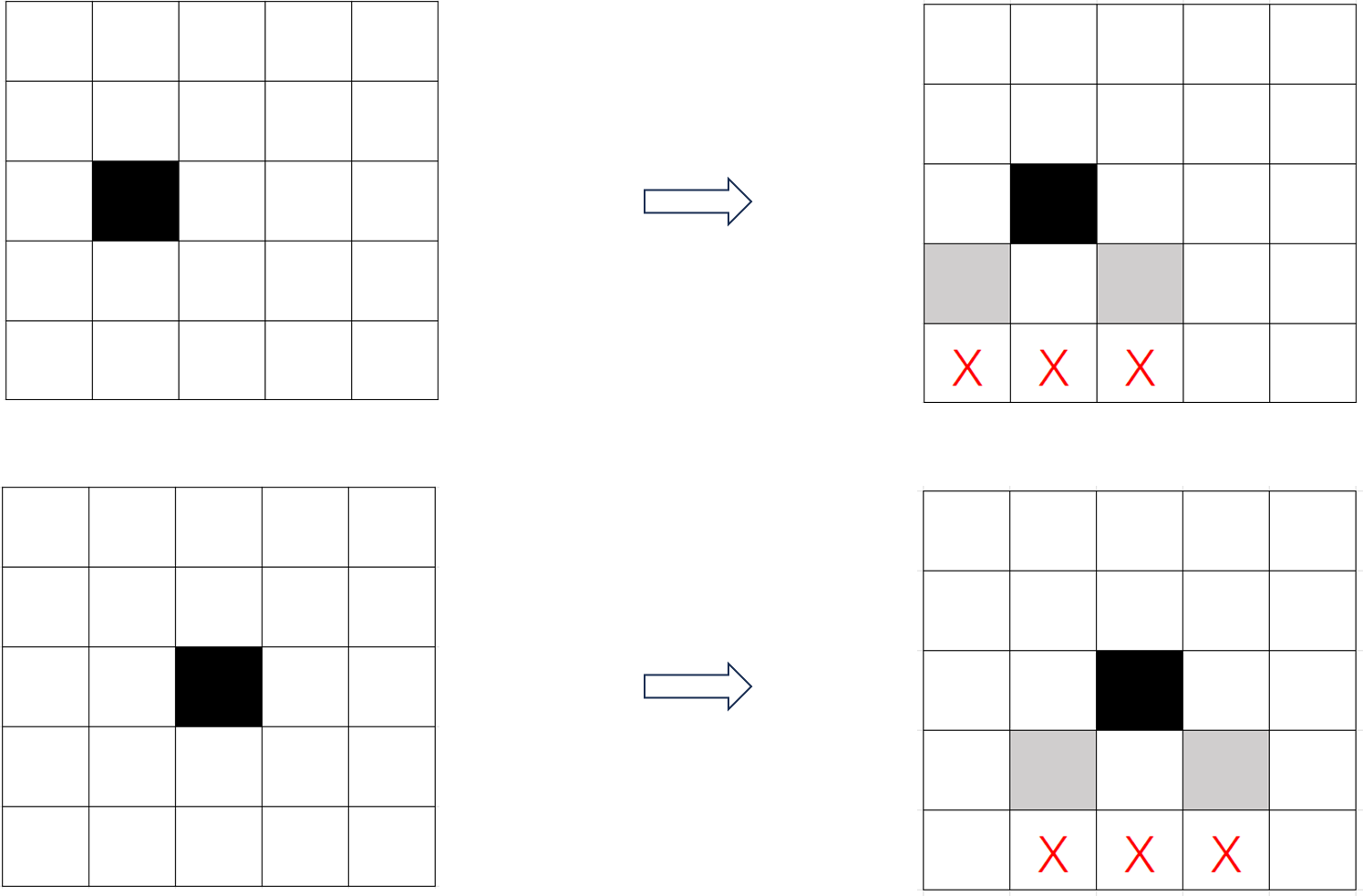
叠加?
$n, k$ 更大时?($k=\lfloor\lceil\frac{1}{2}n\rfloor\rceil - 1$)
-
归纳……
-
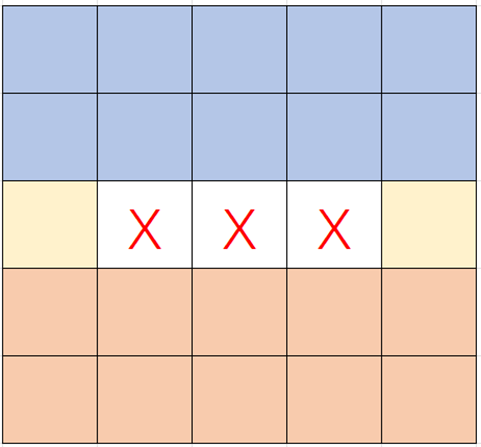
仅考虑最后一条链的分布:
-
红色边框范围内可认为是 $n'=n-2, k'=k-1$ 时的情况
-
最终归纳到 $n=5, k=2$ 时可得一定会有白色格三连,因此无解。
结论
-
$k > \left\lfloor\frac{2}{3}n\right\rfloor$ 时无解。
-
$\left\lceil\frac{1}{2}n\right\rceil \le n \le \left\lfloor\frac{2}{3}n\right\rfloor$ 时可通过组合基本型来构造合法答案;
-
$k < \left\lceil\frac{1}{2}n\right\rceil$ 时……无解
|