更好的阅读体验：https://www.cnblogs.com/To-Carpe-Diem/p/19635135

大意

求前 $k$ 大的互不相同的异或和。

思路

首先，我们将其转换一下，求出前缀异或和，$s$，$s_i = s_i \oplus s_{i - 1} $，这样，对于区间 $[l, r]$ 的异或和询问就变成了 $s_r \oplus s_{l - 1}$。

知道了这个之后，我们的问题现在转化为了，在这 $n$ 个 $s$ 里面选择 $k$ 对，使得其和最大，这个时候，我们要处理的问题是对于 $s_i$ 来说，如何找到一个 $s_j$，使得其 $s_i \oplus s_j$ 的值最大。这个问题十分经典（但是我也刚知道），可以用 Trie 来处理这种动态找最大异或和的问题。

那么如何在 Trie 上维护这个东西呢？我们考虑将每个 $s_i$ 插入 Trie 里面，那么记录每个节点经过的点的个数，我们一定是希望走 $op \oplus 1$ 的位置的，但是如果没有 $op \oplus 1$ 这个位置，就走不了，且，若是左子树的大小不够，也走不了，必须走到 $sz \ge rk$ 的地方，这个才是对的。于是就类似权值线段树静态查第 $k$ 大差不多，不过此题我们要处理的是前 $2k$ 大，因为我们忽略了 $l \le r$ 的限制。

我们只需要用一个大根堆记录即可，但是每个答案都会以 $s_i$ 和 $s_j$ 为基准分别各出现一次，那么最终我们选择的答案需要除以 $2$。

代码

#include<iostream>
#include<queue>
using namespace std;

#define ll long long
const int MAXN = 5e5 + 5;
const int MAXT = MAXN * 32;

int ch[MAXT][2], cnt[MAXT];
ll s[MAXN], tot = 0, n, k;

struct node{
    int id, rk;
    ll val;
    bool operator<(const node &other)const{
        return val < other.val;
    }
};

void Insert(ll x){
    int now = 0;
    for(int i = 31;i >= 0;i --){
        int op = (x >> i) & 1;
        if(!ch[now][op]) ch[now][op] = ++ tot;
        now = ch[now][op];
        cnt[now] ++;
    }
}

ll query(ll x, int rk){
    int now = 0;
    ll res = 0;
    for(int i = 31;i >= 0;i --){
        int op = (x >> i) & 1;
        op ^= 1;
        if(!ch[now][op]){
            now = ch[now][op ^ 1];
        }
        else if(rk <= cnt[ch[now][op]]){
            res |= (1LL << i);
            now = ch[now][op];
        }
        else{
            rk -= cnt[ch[now][op]];
            now = ch[now][op ^ 1];
        }
    }
    return res;
}

int main(){
    cin.tie(0) -> ios::sync_with_stdio(0);
    cin >> n >> k;
    s[0] = 0;
    Insert(s[0]);
    for(int i = 1;i <= n;i ++){
        ll a; cin >> a;
        s[i] = s[i - 1] ^ a;
        Insert(s[i]);
    }
    
    priority_queue<node> q;
    for(int i = 0;i <= n;i ++){
        ll x = query(s[i], 1);
        q.push({i, 1, x});
    }
    ll ans = 0;
    for(int i = 1;i <= 2 * k;i ++){
        node t = q.top();
        ans += t.val;
        q.pop();
        if(t.rk < n){
            q.push({t.id, t.rk + 1, query(s[t.id], t.rk + 1)});
        }
    }
    cout << ans / 2;
    return 0;
}

更好的阅读体验：https://www.cnblogs.com/To-Carpe-Diem/p/19635009

大意

给出 $n$ 张卡牌，每张卡牌都有两个权值 $a_i$ 和 $b_i$，分别对应的是正面和反面，求在至少翻 $m$ 张牌，然后求出最小的极差。

思路

我们考虑这样的事，首先，我们不考虑每一张牌的情况，我们只考虑这个先处理极差的问题，我们先把这 $2n$ 张牌记录一下类型，然后将其排序。

排完序之后，我们需要的是选择一段区间 $[L, R]$，使得 $[L, R]$ 的区间包含所有的类型，且其中间反转的牌不超过 $m$ 个，那么这个区间的 $val_R - val_L$ 就是一个合法的答案，我们要想使得这个值尽可能的小，我们不妨使用双指针的写法，固定左端点，向右查询合法右端点。

这个过程是具有单调性的，你的 $L$ 向右，$R$ 也必定向右，具体过程是这样的，如果当前的区间不合法，那么就让 $R$ 右移，使其包含所有的 $n$ 个情况，一旦包含足够，就判断是否合法，这个过程是可以在扫描的过程中动态处理的，这步判断是 $\mathcal{O}(1)$ 的，如果是合法就将 $L$ 向右收缩，这样去看看有没有更优的 $val_R - val_L$。

代码

#include<iostream>
#include<algorithm>
using namespace std;

const int MAXN = 1e6 + 5;
int n, m, l, r, cnt = 0;
struct node{
    long long val, id;
    bool op;
}k[MAXN << 1];
int t[MAXN << 1];
bool cmp(node x, node y){
    return x.val < y.val;
}

int main(){
    // freopen("card.in", "r", stdin);
    // freopen("card.out", "w", stdout);
    cin.tie(0) -> ios::sync_with_stdio(0);
    cin >> n >> m;
    for(int i = 1;i <= n;i ++){
        cin >> k[i].val;
        k[i].id = i;
        k[i].op = 1;
    }
    for(int i = 1;i <= n;i ++){
        cin >> k[i + n].val;
        k[i + n].id = i;
        k[i + n].op = 0;
    }
    sort(k + 1, k + 2 * n + 1, cmp);
//    for(int i = 1;i <= n * 2;i ++){
//        cout << k[i].val << ' ' << k[i].id << ' ' << k[i].op << '\n';
//    }
    for(l = 0;cnt + k[l + 1].op <= m && !t[k[l + 1].id];l ++){
        cnt += k[l + 1].op;
        t[k[l + 1].id] = 1;
    }
    for(r = 2 * n + 1;cnt + k[r - 1].op <= m && !t[k[r - 1].id];r --){
        cnt += k[r - 1].op;
        t[k[r - 1].id] = 1; 
    }
    long long ans = 1e9 + 7;
	while(l >= 0) {
		ans = min(k[r - 1].val - k[l + 1].val, ans);
		t[k[l].id] = 0;
		cnt -= k[l].op;
		l --;
        for(r;cnt + k[r - 1].op <= m && !t[k[r - 1].id];r --){
            cnt += k[r - 1].op;
            t[k[r - 1].id] = 1; 
        }
	}
	cout << ans << '\n';
}

更好的阅读体验：https://www.cnblogs.com/To-Carpe-Diem/p/19635050

大意

给定一个序列，每个数有两种颜色，要找到一个位置，要找到一个位置使得 $\min \{ f(p), g(p) \}$ 尽可能大.

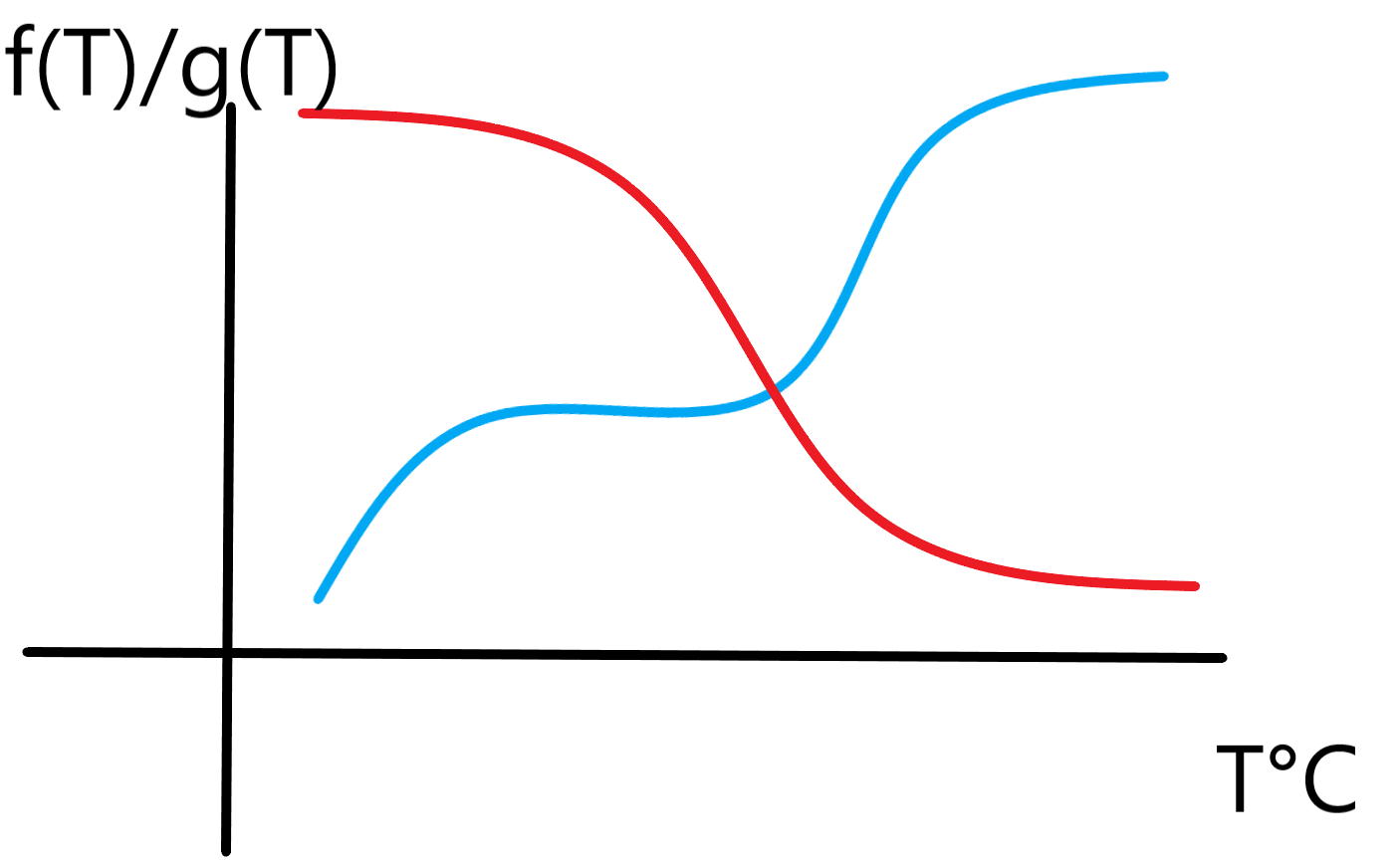
思路

我们在温度 $T$ 下，能参加的冰人必须是 $y \le T$ 的才能参赛，火人必须是 $y \ge T$ 才能参赛，我们定义能参赛的冰人的能量和为 $f(T)$，同理，火人为 $g(T)$。

那么我们的答案一定是 $2 \times \min \{ f(T), g(T)\}$，对于这个图，画出来是下面这样的：

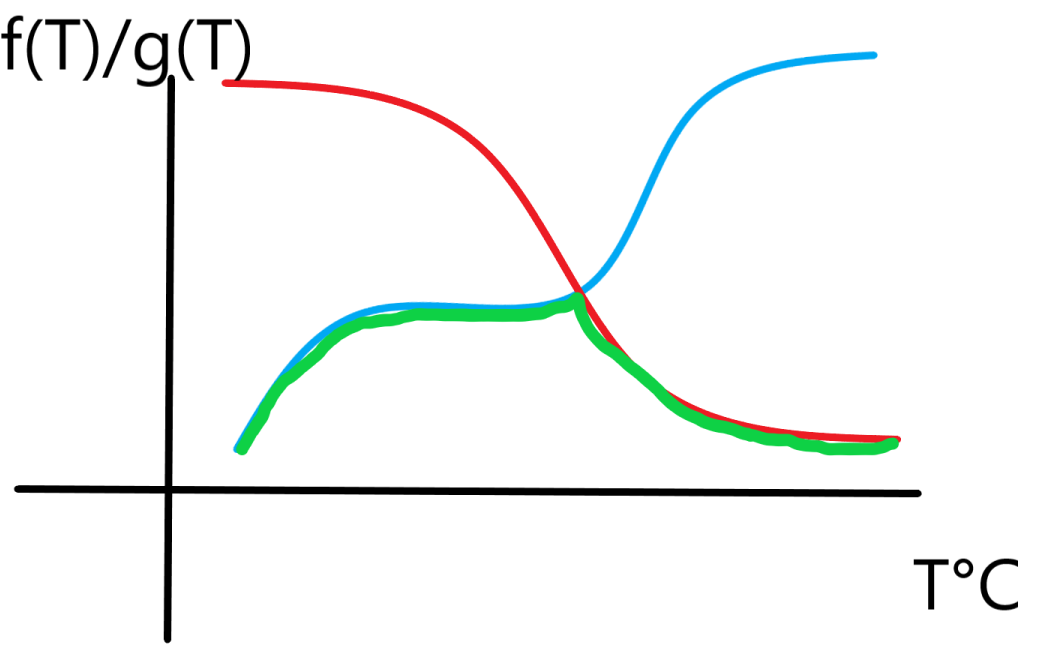
那么，取 $\min$ 之后的图像是这样的：

就是绿色的部分，那么我们这样的话，答案一定在交点附近，那么我们在求这个交点的过程，可以尝试二分 + 树状数组，由于一个是递增，一个是递减，分别维护前缀和和后缀和即可，那么这样二分到交点 $p$ 的话，只需要看 $p$ 和 $p + 1$ 位置，相当于是冰人和火人的位置，火人的位置比较特殊，因为是可能后面还有段连续的区间，需要继续从 $p + 1$ 向右跳到最后一个合法的区间。

而上述的做法，不难发现时间复杂度是 $Q \log^2 Q$ 的，无法通过此题，只能有 $60pts$，于是我们考虑优化。

有个比较经典的思路（不过我也是刚学会的），在树状数组上倍增，这样的话，我们只需要单 $\log$ 的复杂度去跳交点，以及查找 $p + 1$ 的后面最后一个满足情况的点即可。

代码

#include<bits/stdc++.h>
using namespace std;

#define ll long long
const int MAXN = 2 * 1e6 + 5;
ll t1[MAXN], t2[MAXN];
int lsh[MAXN], tot;
ll sum = 0;

struct node{
	int op, t, x, y;
}q[MAXN];

int lowbit(int x){
	return x & -x;
}

void add(ll *bit, int x, ll k){
//	if(x <= 0) return;
	while(x <= tot + 1){
		bit[x] += k;
		x += lowbit(x);
	}
}

int Q;

int main(){
	cin.tie(0) -> ios::sync_with_stdio(0);
	
	cin >> Q;

	for(int i = 1;i <= Q;i ++){
		cin >> q[i].op;
		if(q[i].op == 1){
			cin >> q[i].t >> q[i].x >> q[i].y;
			lsh[++ tot] = q[i].x;
		}
		else{
			cin >> q[i].t;
		}
	}

	sort(lsh + 1, lsh + tot + 1);

	tot = unique(lsh + 1, lsh + tot + 1) - (lsh + 1);

	for(int i = 1;i <= Q;i ++){
		if(q[i].op == 1){
			q[i].x = lower_bound(lsh + 1, lsh + tot + 1, q[i].x) - lsh;
		}
	}

	for(int i = 1;i <= Q;i ++){
		if(q[i].op == 1){
			if(q[i].t == 0) add(t1, q[i].x, q[i].y);
			else add(t2, q[i].x + 1, q[i].y), sum += q[i].y;
		}
		else{
			if(q[q[i].t].t == 0) add(t1, q[q[i].t].x, -q[q[i].t].y);
			else add(t2, q[q[i].t].x + 1, -q[q[i].t].y), sum -= q[q[i].t].y;
		}
		ll p1 = 0, s1 = 0, s2 = 0;
		for(int j = 20;j >= 0;j --){
			int nxt = p1 + (1 << j);
			if(nxt <= tot && s1 + t1[nxt] < sum - (s2 + t2[nxt])){
				p1 = nxt, s1 += t1[nxt], s2 += t2[nxt];
			}
		}
		ll res1 = s1;
		ll res2 = 0, p2 = 0;
		if(p1 < tot){
			ll ss1 = 0, ss2 = 0;
			for(int j = p1 + 1;j;j -= lowbit(j)){
				ss1 += t1[j], ss2 += t2[j];
			}
			res2 = sum - ss2;
			if(res2 >= res1){
				p2 = 0, ss2 = 0;
				for(int j = 20;j >= 0;j --){
					int nxt = p2 + (1 << j);
					if(nxt <= tot && sum - (ss2 + t2[nxt]) >= res2){
						p2 = nxt;
						ss2 += t2[nxt];
					}
				}
			}
		}
		if(res1 == res2 && res1 == 0){
			cout << "Peace\n";
		}
		else if(res1 <= res2){
			cout << lsh[p2] << ' ' << res2 * 2 << '\n';
		}
		else{
			cout << lsh[p1] << ' ' << res1 * 2 << '\n';
		}
	}

	return 0;
}

这集神了。

先考虑一条链怎么做，即求 $\sum_{i=0}^k a_{x+i}\text{ xor } i$。因为先异或后求和，可以考虑拆位来算，不难发现，$\forall j\in [x,x+2^p)$，$a_j$ 的第 $p$ 位都异或上了 $0$，如果我们将第 $p$ 位去掉并只考虑小于 $p$ 位的贡献，不难发现区间分成了 $[x,x+2^{p-1}),[x+2^{p-1},x+2^p)$ 两个子区间，且他们要解决的问题结构完全相同，这启发我们用倍增去解决问题。

设 $f_{i,j}$ 表示只考虑小于 $j$ 位的值对于 $\sum_{p=0}^{2^j-1} a_{i+p}\text{ xor } p$，设 $g_{i,j,0/1}$ 表示 $1\sim i$ 中第 $j$ 位为 $0/1$ 的位置个数，则有：
$$f_{i,j}=f_{i,j-1}+f_{i+2^{j-1},j-1}+(g_{i+2^{j-1}-1,j-1,1}-g_{i-1,j-1,1}+g_{i+2^j-1,j-1,0}-g_{i+2^{j-1},j-1,0})2^{j-1}$$

这个转移式子大概意思是：对于一个长度为 $2^j$ 的区间，先将这个东西小于 $j-1$ 位的贡献求出来，然后考虑第 $j-1$ 位的贡献，前一半区间只有第 $j-1$ 位为 $0$ 能贡献，后一半只有为 $1$ 才能贡献。

然后我们回到询问，从高到低位拆位算贡献，同时倍增跳，能跳就跳，不能跳就将当前位置到终点部分剩余位置在当前拆的这一位上的贡献算出来。

for(int j=30;j>=0;j--){
	if((k>>j)&1){
		nxt=u+(1<<j);ans+=f[j][u];
		c1=g[1][j][nxt-1]-g[1][j][u-1];
		c0=g[0][j][r]-g[0][j][nxt-1];
		ans+=(c1+c0)*(1ll<<j);u=nxt;
	}else{
		ans+=(g[1][j][r]-g[1][j][u-1])*(1ll<<j);
	}
}

具体的，我们将倍增数组 $f_{i,j}$ 的定义改为从 $i$ 到 $i$ 所在长链往下 $2^j$ 步。对于轻重儿子合并，可以直接将轻儿子的倍增数组加到重儿子的倍增数组上，然后直接对当前点的 $\log$ 个位置倍增。对于 $g$ 也这样更改定义，但是从前缀和变成了后缀和，这样可能会出现很多问题：如倍增数组空位无法合并，后缀和可能访问到不该访问的值，但总而言之是小问题，模仿上面的倍增过程跳下去即可。

时间复杂度为 $O(n\log V)$。