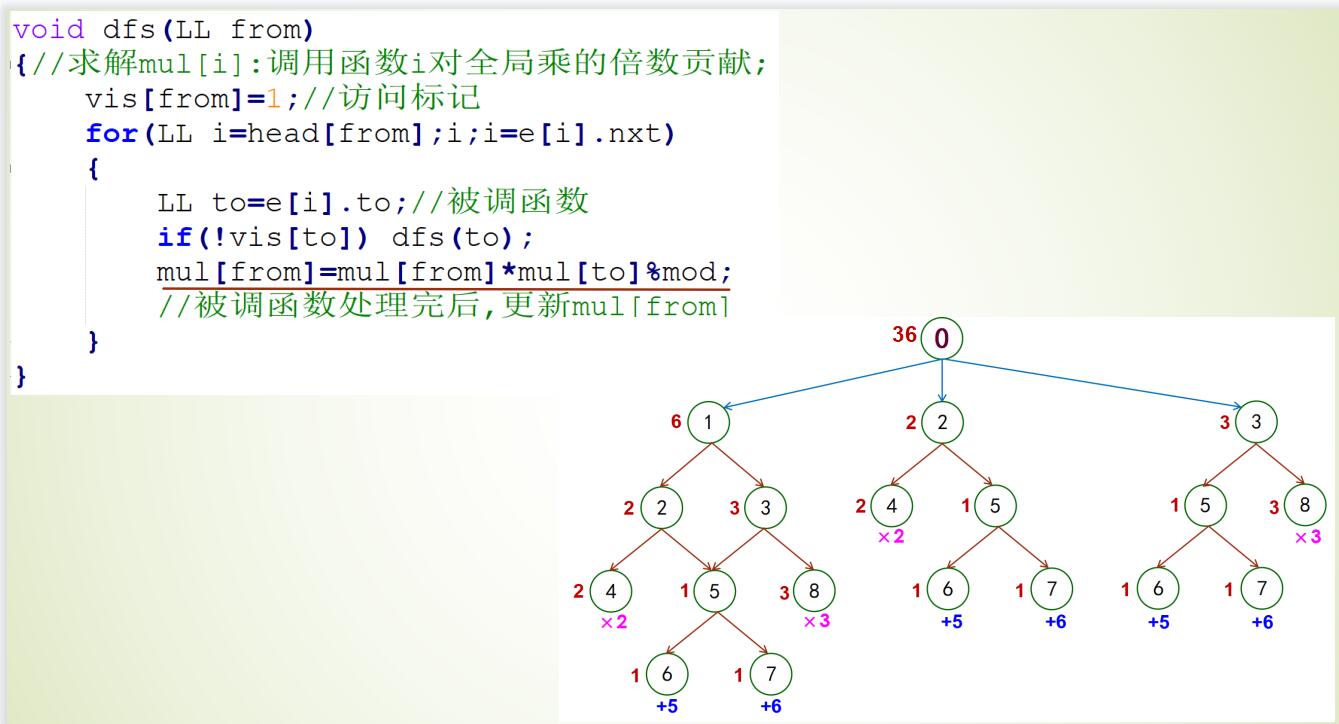
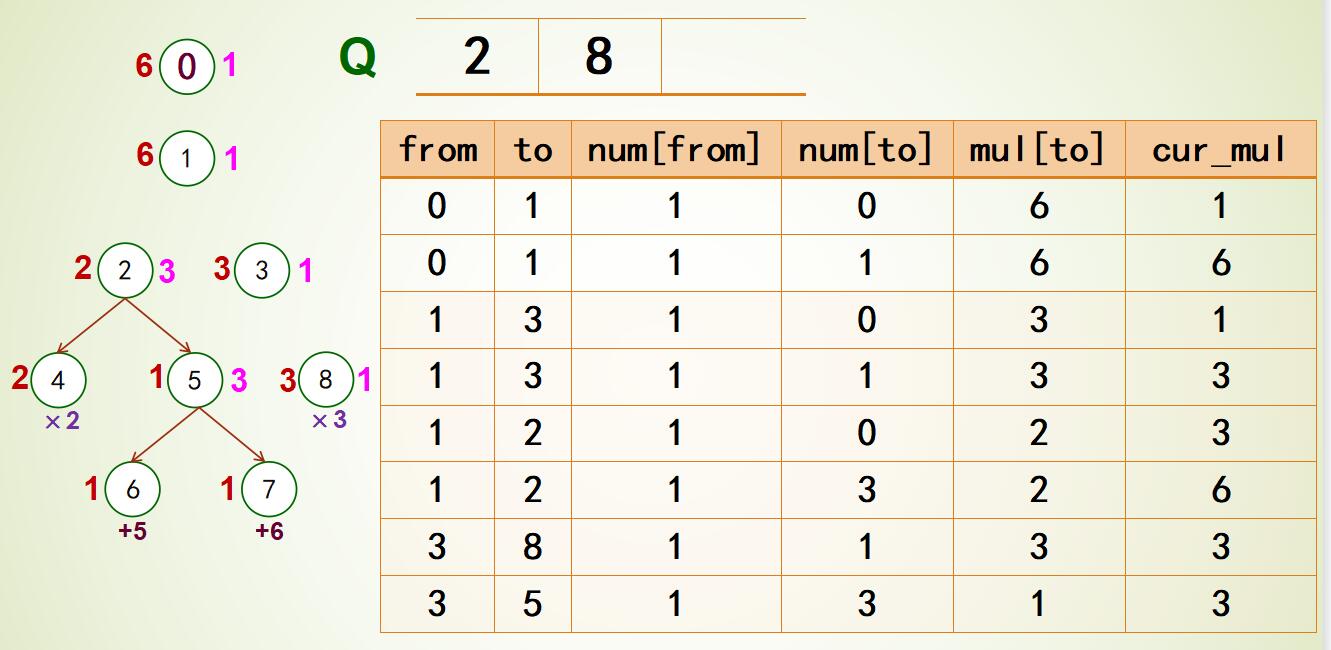
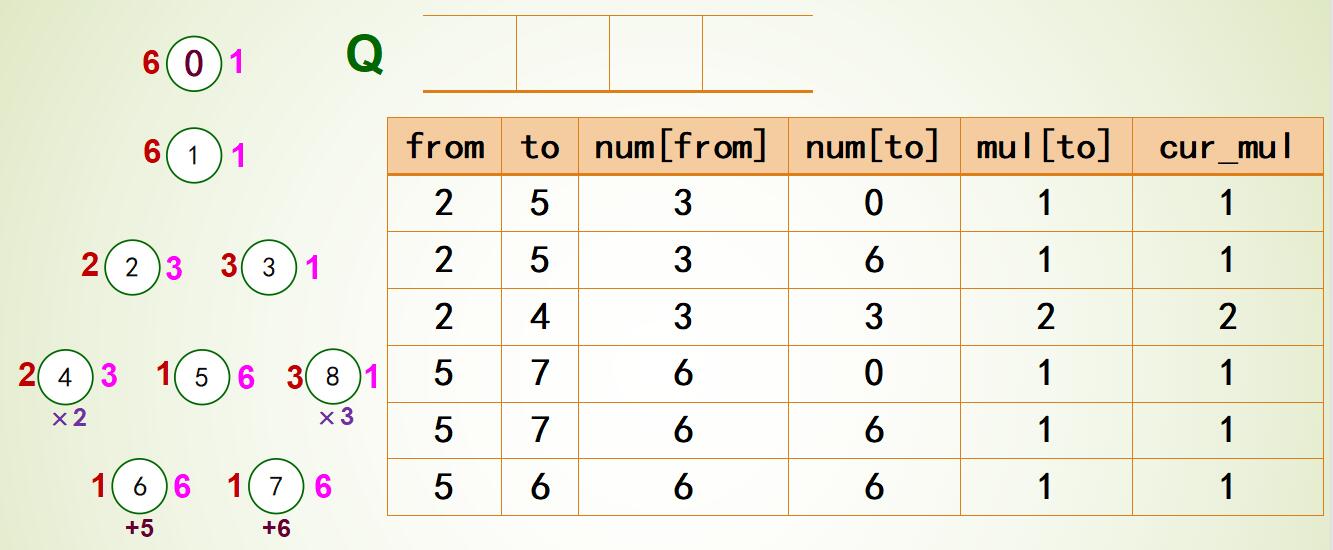
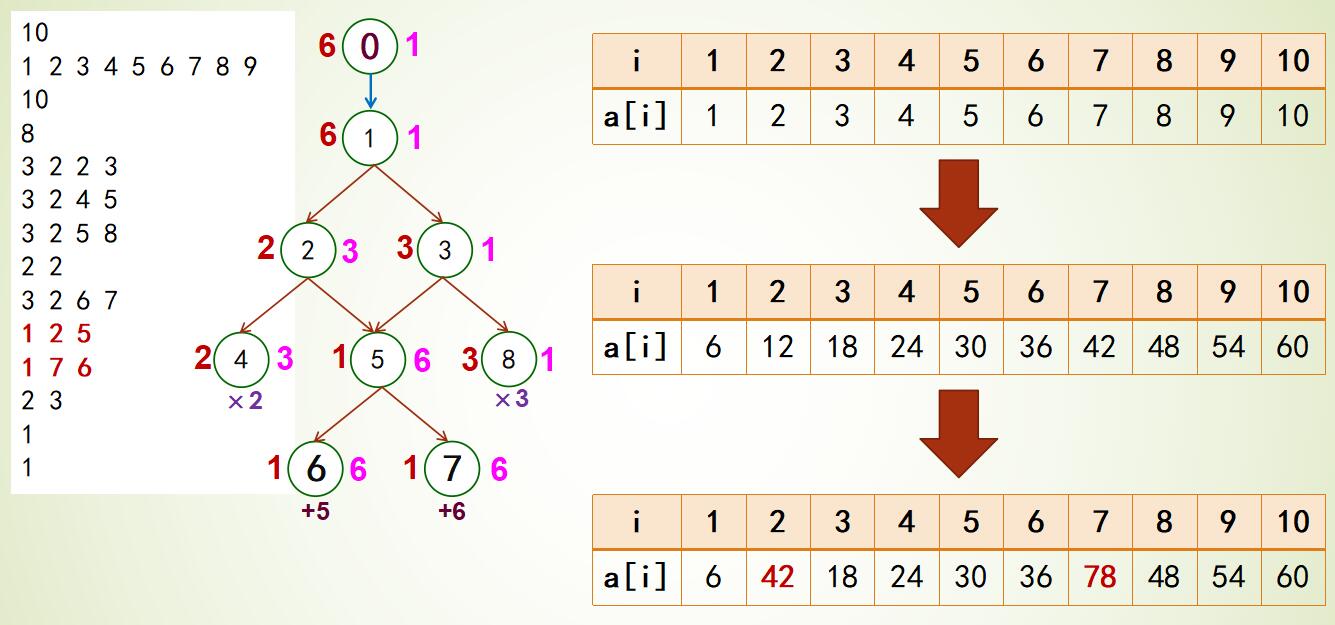
|
|
题目3504 [CSP 2020S]函数调用
AAAAAAAAAAAAAAAAAAAA
 10
评论 10
评论
2022-06-14 11:24:09
|
|
|
不想写whk作业了来补一补之前没写出来的题。。。 当时做这题的时候一直在想有没有什么贪心方法,结果到最后没想出来,后来一看标签是动规,很快就写出来了。 状态转移方程很好想, $f(i, j) \iff f_{i, j} \\f(i, j) = \begin{cases} S(1, i) &\text{if} \ j = 0 \\ \displaystyle{\min_{j - 1}^{i - 1}(f(k, j - 1) + S(k+ 1, i))} &\text{otherwise} \end{cases}$ 其中 $f(i, j)$ 表示在前 $i$ 个数字中共添加 $j$ 个加号时的最小值
题目124 [NOI 1996]添加号
AAAAAAAAAA
 7
评论 7
评论
2022-06-06 13:26:23
|
|
|
完整版实在是太长了,所有分析就列在博客里了,这里简述 AC 做法。 不难观察到最后一段和越小答案越小。 令 $dp(i)$ 为 $i$ 结尾时的最小取值,$pos_i$ 为 $i$ 取得最小值时所处段前一段的最后一个元素。 有 $dp(i) = dp(pos_i) + (s_i - s_{pos_i})^2$ 求出 $a$ 的前缀和数组 $s$。 用一个单调队列维护 $2\times s_j - s_{pos_j}$,当队首和队首后一个元素都满足 $2 \times s_j - s_{pos_j} \le s_i$ 时,循环删除队首。 由于数据很大,只存储 $pos$ 数组,答案最后统一计算即可。
题目3293 [CSP 2019S]划分
AAAAAAAAAAAAAAAAAAAAAAAAA
 8
评论 8
评论
2022-05-28 23:07:14
|
|
|
搬这题只是为了庆祝窝洛谷过审的第一篇题解awa 首先这种格式一看就是要用数据结构维护,但我们会发现由于 $a$ 数组和 $k$ 的值都是变化的,普通数据结构几乎难以维护。 遇到这种问题,我们可以尝试往分块或者根号分治上想。 顺着这个思路,考虑寻找一下答案的性质。 发现当 $k \gt \sqrt{N}$ 时,操作时间复杂度最多只有 $O(\sqrt{N})$。 那要是 $k \le \sqrt{N}$ 怎么办? 这个时候 $k$ 已经非常小了,我们可以把 $k \le \sqrt{N}$ 的每一种情况都预处理出来。 在询问时,若 $k \gt \sqrt{N}$ 时,直接暴力模拟,反之直接输出我们预处理的结果就好了。 相当于用空间换时间,二者复杂度均为 $O(N\sqrt{N})$。
根号分治的有趣运用还有很多,这道题基本上相当于模板,还有一道类似的题目 哈希冲突 可以尝试做一做,cb 大佬的题解
题目3670 [Codeforces 797E]Array Queries
AAAAAAAAAAAAAAAAAAAA
 5
评论 5
评论
2022-05-28 12:37:48
|
|
|
看到这道题,最朴素的想法是用 DFS 求解。 显然这样搜出来的状态数量非常庞大,时间复杂度无法承受,考虑换用 DP 遍历所有状态。 这里有两个方法。 法一:(60pts) 设 $f_i$ 表示正整数 $i(i \in N^+)$ 分解后的最大乘积。 这种情况下乍一看似乎无法转移,因为有后效性,前面的数分解出 $k$ 那么后面就不能分解出 $k$ 了。 既然如此,可以尝试改变状态,多加几维限制。 思考后得出:设 $f(i,j)$ 表示正整数 $i(i \in N^+)$ 分解出的最大整数为 $j$ 时的最大乘积。 初始状态:$\forall i \in [0,n],f(0,i) = 1$ 状态转移方程:$f(i,j) = \max\limits_{k=1}^{j - 1} f(i - j,k) \times j$ 最终状态 $\max\limits_{i=0}^n f(n,i)$ 然而这样是 $O(N^3)$ 的,考虑优化。 令 $s(i,j) = \max\limits_{k=1}^j f(i,k)$ 则状态转移方程会变成:$f(i,j) = s(i - j,j - 1) \times j$ 初始 $\forall i \in [0,n],s(0,i) = 1$ 答案为 $s(n,n)$ 这样用 unsigned long long 可以过 $60%$ 的测试数据,但换成高精度则会出现一堆绿色的字母。 (upd:测试时发现,其实根据数学知识,每次转移的 $j$ 并不会太大,有兴趣的可以打个表把 $j$ 的范围缩小些,这样应该能直接 AC)
法二: (此方法我暂时给不出严谨的证明,只能感性理解给个大概意思) 再仔细想一想,难道这个 DP 就一定要二维吗? 再想一想,假设我们把 $i$ 分解为 $\{a_1,a_2\ldots a_k \}$,要枚举一个 $a_j(1\le j \le k)$ 进行状态转移。 不难发现,每个数字分别顺序的先后并不影响它对答案的贡献。 换言之,不论枚举的顺序如何,最优状态也一定会被遍历到。 基于此,我们令 $f_i$ 为 $i$ 分解的最优答案,用 bitset 或者 bool 数组记录一下哪些数字被选上了,转移一下就好了。 这个转移方程相当简单,就不写了,详情见 AC 代码。
题目618 [金陵中学2007] 最优分解方案
AAAAAAAAAA
 12
2 条 评论 12
2 条 评论
2022-05-20 21:16:44
|
|
|
原式可以化为 $\displaystyle{\sum_{p \in primes}\sum_{i = 1}^n\sum_{j = 1}^m[(i, j) = p]}$ 注意到,$[(i, j) = p] = [\frac{(i, j)}{p} = 1] = [(\frac{i}{p}, \frac{j}{p}) = 1]$,因此原式进一步化为 $\displaystyle{\sum_{p \in primes}\sum_{i = 1}^n\sum_{j = 1}^m\sum_{d \mid (\frac{i}{p}, \frac{j}{p})}\mu(d)}$ 我们交换求和顺序,有 $\displaystyle{\sum_{p \in primes}\sum_{d = 1}\mu(d)\sum_{i = 1}^n[d \mid \frac{i}{p}]\sum_{j = 1}^m[d \mid \frac{j}{p}]}$ 注意到,$1 \sim \frac{n}{p}$ 中 $d$ 的倍数有 $\left \lfloor \frac{\frac{n}{p}}{d} \right \rfloor = \left \lfloor \frac{n}{dp} \right \rfloor$ 个,因此有 $\displaystyle{\sum_{p \in primes}\sum_{d = 1}^{\min(\frac{n}{p}, \frac{m}{p})}\mu(d) \left \lfloor \frac{n}{dp} \right \rfloor\left \lfloor \frac{m}{dp} \right \rfloor}$ 令 $t = dp$,我们在外层枚举 $t$ $\displaystyle{\sum_{t = 1}^{\min(n, m)} \left \lfloor \frac{n}{t} \right \rfloor\left \lfloor \frac{m}{t} \right \rfloor \sum_{p \in primes, p \mid t} \mu(\frac{t}{p})}$ 我们维护一个 $\mu$ 的前缀和就可以了,具体来说,我们维护一个数组 $S$ ,枚举 $p, t$ ,如果 $p \mid t$ 就令 $S_k \gets S_k + \mu(\frac{t}{p})$,然后接下来就正常的维护前缀和就行了。
注意该题数据规模很大,需要进行一些优化(比如不该开 long long 的地方用 int)。
题目2165 [BZOJ 2820] YY的GCD
AAAAAAAAAA
 8
评论 8
评论
2022-05-08 14:15:39
|