|
|
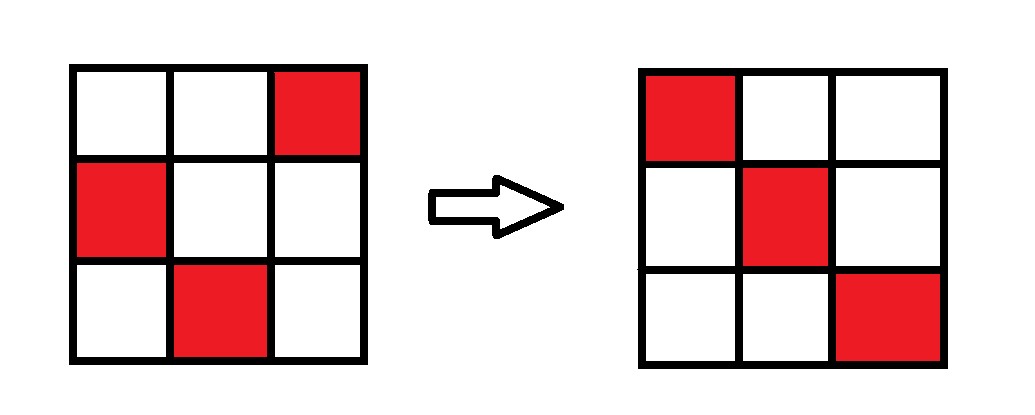
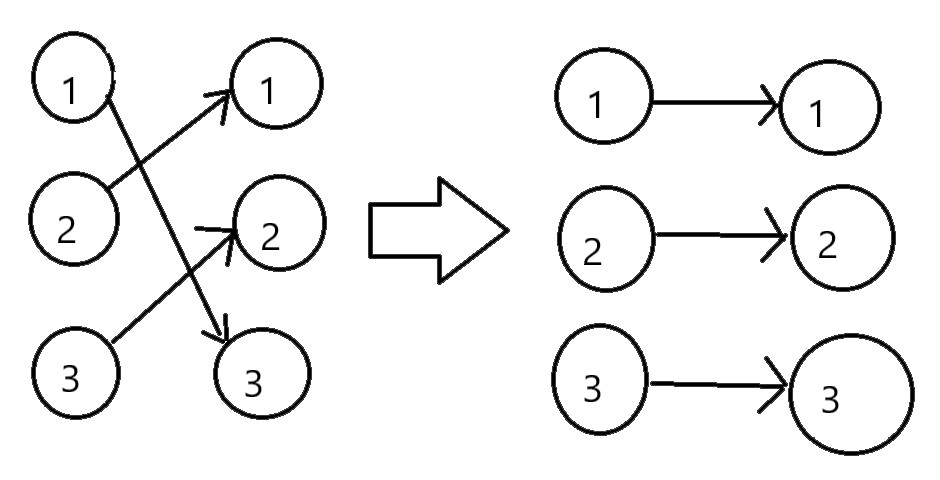
题目3055 [NOIP 2018]赛道修建
 2
评论 2
评论
2024-10-24 23:23:50
|
|
|
 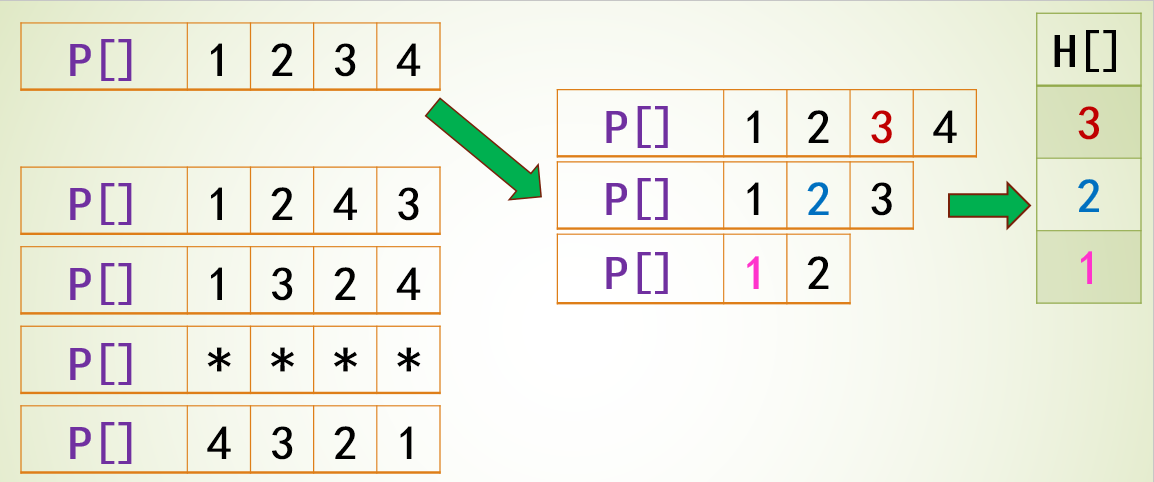  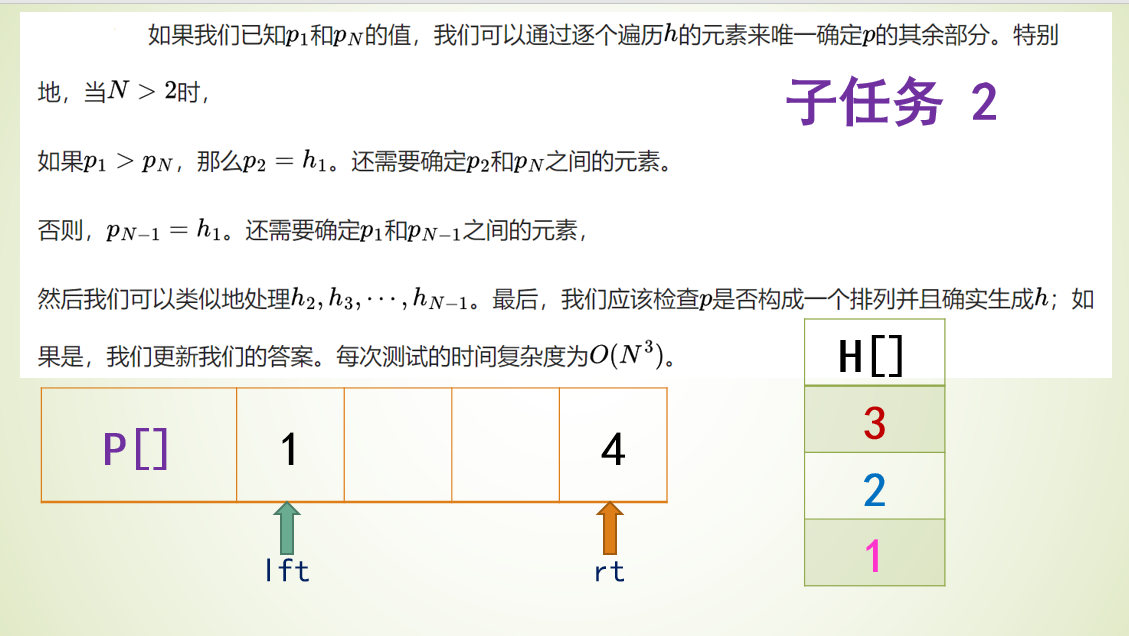 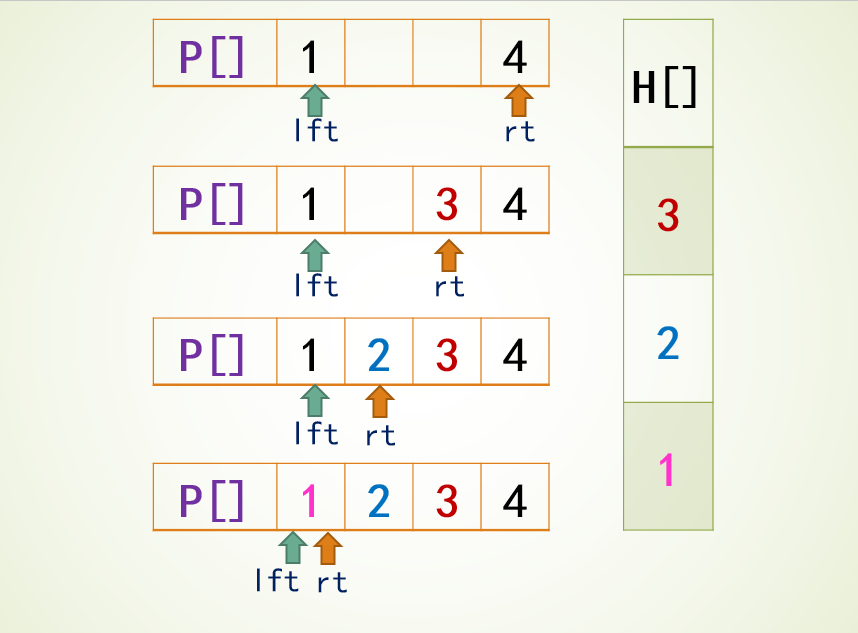   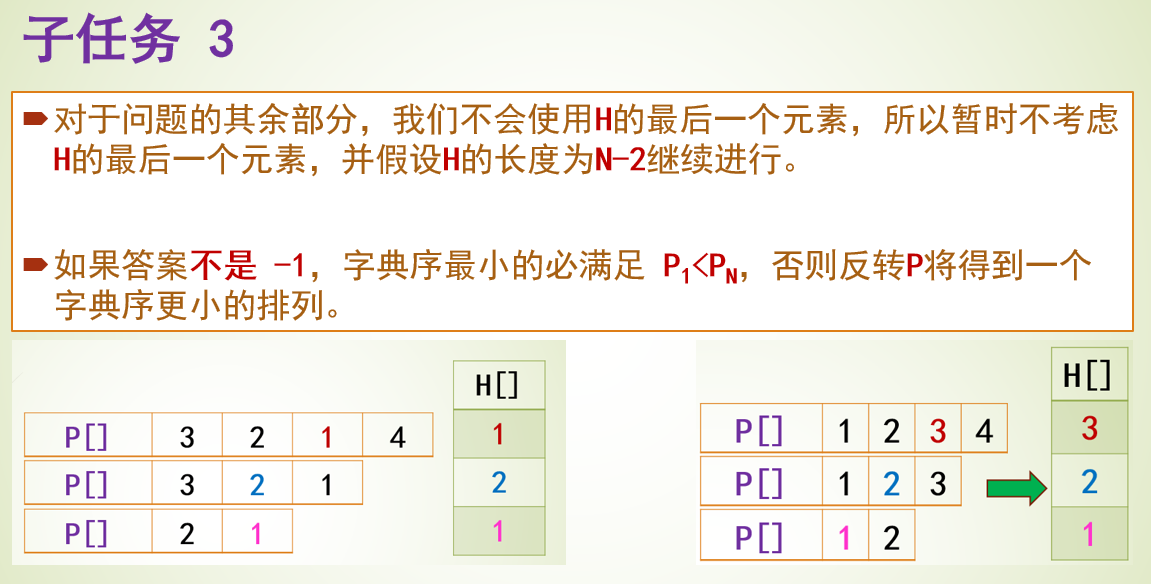   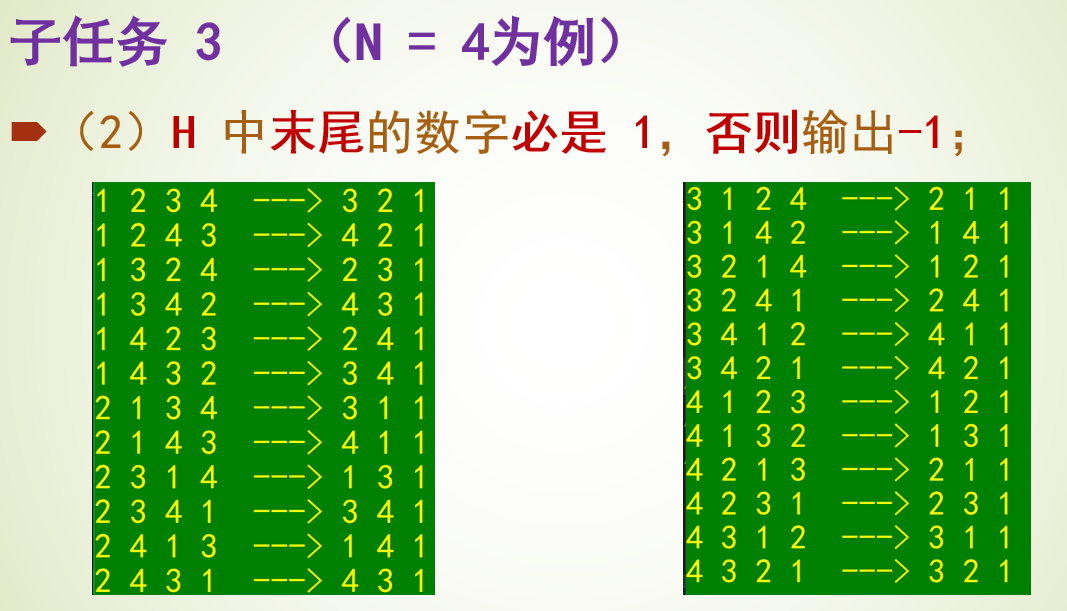      
题目4031 [USACO24 Open Bronze]Farmer John’s Favorite Permutation
 2
评论 2
评论
2024-10-24 12:32:02
|
|
|
题目3827 举办乘凉州喵,举办乘凉州谢谢喵
 5
评论 5
评论
2024-04-03 12:11:51
|
|
|
__int128类型使用方法该题大整数运算部分,可以使用 __int128 类型,该类型需要 自定义输入输出,详细方法请参考如下代码: #include <bits/stdc++.h>
using namespace std;
typedef __int128 LL;
inline read(LL &x)//输入
{
x = 0;
LL f = 1;
char ch;
if((ch = getchar()) == '-')
f = -f;
else
x = x*10 + ch-'0';
while((ch = getchar()) >= '0' && ch <= '9')
x = x*10 + ch-'0';
x *= f;
}
inline print(LL x)//输出
{
if(x < 0)
{
x = -x; putchar('-');
}
if(x>9) print(x/10);
putchar(x%10+'0');
}
int main()
{
LL a, b;
read(a); read(b);
print(a + b);
return 0;
}
题目3508 [NOIP 2020]排水系统
 9
2 条 评论 9
2 条 评论
2023-10-27 14:04:50
|
|
|
题目660 [ZJOI 2007] 矩阵游戏
 5
评论 5
评论
2023-03-24 20:38:28
|
|
|
差分约束模板题 本题求最小值,需构造 $\ge$ 不等式组,构图求最长路,如果存在正环,则说明无解。 分析给定的 $5$ 个条件: (1) $A==B \iff A-B \ge 0\ ,\ B-A \ge 0$; (2) $A<B \iff B \ge A + 1\ ,B-A\ \ge 1$; (3) $A \ge B \iff A-B\ \ge 0$; (4) $A > B \iff A \ge B + 1\ ,A-B \ge 1$; (5) $A \le B \iff B \ge A , B-A \ge 0$; 另外还有一隐含条件: 每个小朋友都要分到糖果,因此 $x_i \ge 1$。我们可以建立一个超级源点 $x_0 = 0$,则有: $x_i\ ≥\ x_0 + 1 , x_i\ -\ x_0\ \ge 1$,即从0号点到其他所有点连边,边权为1,因为这样可确保到达任意点,到达任意边,满足所有不等式。 因为我们能求出每个 $x_i$ 的最小值,所以总体最小值就是所有的 $x_i$ 之和。
构图建边数: 如果 $K$ 取 $10^5$,假设所有的条件都是($1$),则需要 $2 \times 10^5$ 条边,从超级源点建边,需要 $10^5$ 条,因此边数预估需要 $3 \times 10^5$ 条边。 另外如果每个小朋友的糖果数是单调递增的,则结果可能爆 $int$,因此需要使用 $long\ long$ 存储结果。
题目3855 [SCOI2011] 糖果
 5
评论 5
评论
2023-03-22 21:30:55
|