| 题目名称 | 2204. [USACO Jan16]愤怒的奶牛 |
|---|---|
| 输入输出 | angry.in/out |
| 难度等级 | ★★★ |
| 时间限制 | 1000 ms (1 s) |
| 内存限制 | 256 MiB |
| 测试数据 | 10 |
| 题目来源 |
|
| 开放分组 | 全部用户 |
| 提交状态 | |
| 分类标签 | |
| 分享题解 |
| 通过:7, 提交:18, 通过率:38.89% | ||||
|
|
100 | 0.094 s | 0.86 MiB | C++ |
|
|
100 | 0.102 s | 0.89 MiB | C++ |
|
|
100 | 0.103 s | 0.89 MiB | C++ |
|
|
100 | 0.271 s | 0.31 MiB | C++ |
|
|
100 | 1.203 s | 0.48 MiB | C++ |
|
|
100 | 3.201 s | 0.88 MiB | C++ |
|
|
100 | 3.254 s | 0.88 MiB | C++ |
|
|
90 | 0.102 s | 0.89 MiB | C++ |
|
|
70 | 0.004 s | 0.31 MiB | C++ |
|
|
70 | 0.097 s | 7.94 MiB | C++ |
| 本题关联比赛 | |||
| 4043级NOIP2022欢乐赛7th | |||
| 关于 愤怒的奶牛 的近10条评论(全部评论) | ||||
|---|---|---|---|---|
|
回复 @zhengtn03 :
有可能是这个问题,我现在感觉我的三分有可能是不完全对的,只是恰好数据水?但是答案都是十分接近的 | ||||
|
第四组 x=654512559.5 时,r=34168.5
错的原因可能是r随x变化不是严格凸的?存在既不增也不减的情况?存在平行于x轴的情况?
2016-04-02 02:33
2楼
| ||||
|
第四组实在过不了,跟答案差了0.5.......怎么都调不过,怒cheat
官方题解:DP/贪心 One approach for solving this problem is by combining a left-to-right scan with a right-to-left scan (one could call each scan either greedy or an example of dynamic programming). We first run a greedy/DP algorithm from left to right to determine for each hay bale the minimum power with which it must explode in order to propagate all the way left. We then do the same from right to left, computing for each hay bale the minimum power with which it must explode in order to propagate all the way to the right. Finally, by scanning through the list of hay bales, we can use these two numbers to identify the best "crossover" point where we should set the initial explosion. Here is Mark Gordon's remarkably concise solution. Note how he uses a couple of clever tricks -- for example to run the algorithm from right to left, he simply reverses the input, runs the left-to-right algorithm, then reverses the output so it appears in the forward direction. Note also how he multiplies all haybale locations by 2 initially so only integer math is required; this eliminates any possibility of rounding error from using floating point numbers. This is why, for example, Mark uses "2 + max(..." in his final loop, since it would normally be "1 +" but the numbers are still scaled up by 2. 我的做法:三分奶牛的位置,二分爆炸半径 原因:我们不妨设某个位置最小的爆炸半径为R=F(X),X为位置,我们通过调试发现,F(X)是一个单峰函数(先减小后增大) 于是可以三分奶牛的位置, 我们又发现,R半径越大肯定“越能全部爆炸”,所以我们对于三分给出的位置,可以二分找出最小的爆炸半径,找出离这个位置最近的两个干草堆(我用的是对原数组排序后二分查找,set也可以)向左右两个方向模拟“爆炸”,注意当半径衰减为0或者没有新的草堆爆炸时要立即跳出(这是一个巨大的常数优化),再加上诸多的不合法状态,这样check(X,R)的复杂度就比O(n)小很多,就能水过这道题了 我跑得快的一个上面有注释 设最大的干草堆为M 我的复杂度最坏为O(n*log2(M)*2log3(M)) 但是O(n)的这个因子实际上远远达不到,所以能写过 | ||||
【题目描述】
奶牛 $Bessie$ 设计了一款电子游戏:”愤怒的奶牛”,她认为这将是下一个爆火的游戏。玩家在一个一维场景中用弹弓射奶牛,还包括位于数轴上不同位置的几堆干草。
奶牛 $Bessie$ 使用足够的能量去引爆她所在位置的干草,这将会造成一系列连锁反应使得额外的干草爆炸,$Bessie$ 目标是令所有干草爆炸。
数轴上不同的位置有 $N$ 堆干草,坐标分别为 $X_1,X_2,X_3……X_n$。如果奶牛在位置 $X$ 释放 $R$ 的能量,将会引爆 $[X-R , X+R]$ 范围内的所有干草堆,这些干草堆将同时爆炸,释放 $R-1$ 的能量,将会引起 $[X-(R-1),X+(R-1)]$ 范围内的干草堆发生爆炸,这些干草堆将会继续同时爆炸,释放 $R-2$ 的能量,以此类推。
译者注:能量不会小于 $0$,最少衰减到 $0$。
请找出 $R$ 的最小值。
【输入格式】
输入第一行有一个整数 $n$;
接下来 $n$ 行,每行一个整数 $X_i$,表示第 $i$ 堆干草的坐标;
【输出格式】
输出只有一个实数,为半径 $R$ 的最小值,精确到小数点后 $1$ 位。
【样例1输入】
5 8 10 3 11 1
【样例1输出】
3.0
【样例1解释】
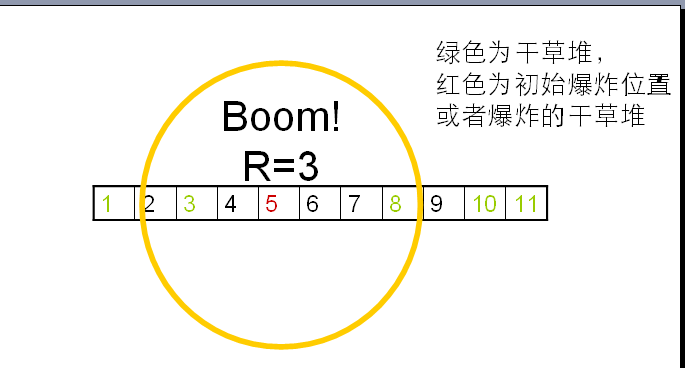
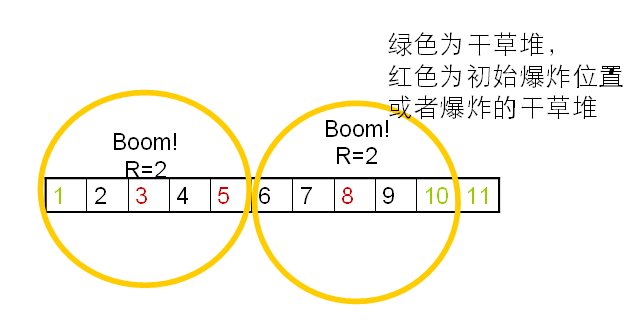

在这个例子中,奶牛在位置 $5$ 释放 $3$ 的能量使得位置 $3$ 和位置 $8$ 的干草堆爆炸,能量衰减为 $2$,位置 $3$ 和位置 $8$ 的干草堆使得位置 $1$ 和位置 $10$ 的干草堆爆炸,能量衰减为 $1$,使得位置 $11$ 爆炸,能量衰减为 $0$。
【样例2输入输出】
点击下载样例2
【数据规模与约定】
对于 $30\%$ 的数据,$N \leq 10$;
对于 $100\%$ 的数据,$N \leq 50000 , X_i \leq 10^9$;